Za usmereni graf kažemo da je jako povezan (engl. strongly connected) ako je svaki čvor grafa dostižan iz svakog drugog čvora u grafu.
Na skupu čvorova usmerenog grafa \(G=(V, E)\) može se definisati relacija \(\sim\) obostrane dostižnosti: \(u\sim v\) ako je čvor \(u\) dostižan iz čvora \(v\) i čvor \(v\) je dostižan iz čvora \(u\). Po definiciji za svaki čvor \(u\) važi \(u\sim u\) (napomenimo da to ne znači da u grafu postoje petlje). Primetimo da su dva čvora obostrano dostižna ako i samo ako pripadaju nekom zajedničkom usmerenom ciklusu. Za relaciju obostrane dostižnosti važi da je:
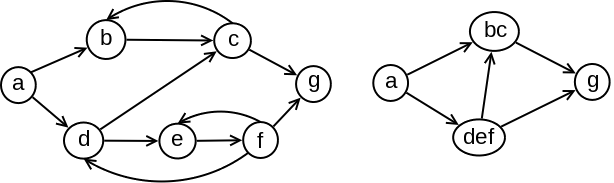
Relacija obostrane dostižnosti je stoga relacija ekvivalencije. Ona razlaže skup čvorova \(V\) u klase ekvivalencije koje nazivamo komponentama jake povezanosti grafa \(G\) (engl. strongly connected components). Na slici 1 (levo) prikazan je usmereni graf \(G\) koji ima četiri komponente jake povezanosti, koje se sastoje redom od čvorova \(\{a\}\), \(\{b,c\}\), \(\{d,e,f\}\) i \(\{g\}\).

Komponente jake povezanosti u grafu imaju razne primene. Razmotrimo primer društvene mreže u kojoj korisnici mogu pratiti akcije drugih korisnika. Potrebno je identifikovati grupe korisnika koji su tesno povezani jedni sa drugima: svako od njih prati svakog drugog, direktno ili indirektno. Ovaj problem odgovara problemu određivanja komponenti jake povezanosti u grafu u kome su korisnici čvorovi, a usmerene grane odgovaraju relaciji praćenja korisnika. U softverskim sistemima moduli se mogu predstaviti čvorovima, a zavisnosti među njima usmerenim granama grafa. Identifikovanje komponenti jake povezanosti pomaže u pronalaženju ciklusa ili potencijalnih problema u strukturi međuzavisnosti modula, koji mogu biti od pomoći u unapređenju dizajna softvera.
Od grafa \(G\) može se formirati kondenzovani ili komprimovani graf \(G^C\): to je usmereni aciklički graf koji sadrži informacije o komponentama jake povezanosti grafa \(G\) (slika 1, desno). Naime, svaki čvor u grafu \(G^C\) odgovara jednoj komponenti jake povezanosti grafa \(G\), a dva čvora u grafu \(G^C\) su povezana granom ako i samo ako u grafu \(G\) postoji bar jedna grana od nekog čvora prve komponente do nekog čvora druge komponente jake povezanosti. Jasno je da je graf \(G^C\) aciklički: ako bi u njemu postojao ciklus, to bi značilo da se sve komponente jake povezanosti koje pripadaju ciklusu mogu spojiti u jednu, veću komponentu jake povezanosti. U nastavku teksta ćemo komponente jake povezanosti zvati kraće samo komponente.
Rešavamo sledeći problem.
Problem. Za dati usmereni graf \(G = (V, E)\) odrediti sve komponente jake povezanosti.
U nastavku teksta razmotrićemo nekoliko varijanti algoritma za rešavanje ovog problema zasnovanih na obilasku iz svakog čvora, a zatim i Tardžanov algoritam i Kosaradžuov algoritam.
U narednom apletu možete proveriti svoje razumevanje komponenata jake povezanosti.
Komponenta jake povezanosti kojoj pripada čvor \(v\in V\) može da se odredi tako što se za svaki čvor \(u\) dostižan iz \(v\) pokrene DFS obilazak sa ciljem da se ustanovi da li je \(v\) dostižan iz \(u\). Postupak se zatim može ponoviti za čvorove koji ne pripadaju prethodno izdvojenim komponentama (ako takvi čvorovi postoje). Postupak je neefikasan jer zahteva veliki broj pokretanja algoritma DFS.
Opisani postupak može se usavršiti. Neka je \(G^*\) graf koji sadrži iste čvorove kao graf \(G\), ali suprotno usmerene grane: grana \((v,u)\) pripada grafu \(G^*\) ako i samo ako grana \((u,v)\) pripada grafu \(G\) (videti sliku 2). Ovaj graf zvaćemo transponovanim grafom (engl. transpose graph) grafa \(G\). Komponente možemo da odredimo i na sledeći način: pokrenemo DFS obilazak iz čvora \(v_0\) u oba grafa, \(G\) i \(G^*\). Prvi DFS obilazak pronalazi skup čvorova \(A\) koji su dostižni iz čvora \(v_0\), a drugi DFS obilazak skup čvorova \(B\) iz kojih je dostižan čvor \(v_0\). Komponenta jake povezanosti kojoj pripada čvor \(v_0\) jednaka je \(A\cap B\). Ovaj postupak ponavljamo za proizvoljni čvor koji ne pripada do sada određenim komponentama povezanosti, ukoliko takav čvor postoji. Najgori scenario je kada su svi čvorovi zasebne komponente i tada je složenost \(O(|V|(|V| + |E|))\).
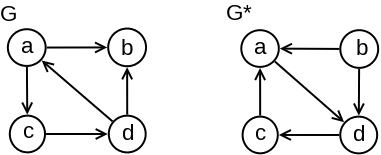
Primer 2.6.1. Razmotrimo grafove \(G\) i \(G^*\) prikazane na slici 2: DFS obilazak grafa \(G\) pokrenut iz čvora \(d\) obilazi skup čvorova \(A=\{d,a,b,c\}\), dok DFS obilazak grafa \(G^{*}\) pokrenut iz čvora \(d\) obilazi skup čvorova \(B=\{d,c,a\}\). Važi \(A\cap B=\{d,a,c\}\), te čvorovi \(d\), \(a\) i \(c\) pripadaju istoj komponenti jake povezanosti. Primetimo da jedino čvor \(b\) ne pripada istoj komponenti povezanosti kao čvor \(d\), a pošto DFS obilazak iz čvora \(b\) u grafu \(G\) obilazi samo čvor \(b\) (jer je njegov izlazni stepen \(0\)), to čvor \(b\) čini sam za sebe drugu (preostalu) komponentu jake povezanosti grafa \(G\).
Postoji nekoliko različitih algoritama linearne vremenske složenosti za određivanje komponenti jake povezanosti u usmerenom grafu, a najpoznatiji među njima su Tardžanov algoritam i Kosaradžuov algoritam. Oba algoritma su zasnovana na DFS obilasku grafa, samo se kod Tardžanovog algoritma sve radi u jednom prolazu kroz graf, dok se u Kosaradžuovom algoritmu dva puta poziva algoritam DFS.
Kao što je to često slučaj kod grafovskih algoritama i izdvajanje komponenata jake povezanosti se zasniva na pažljivoj analizi DFS drveta i njegovih osobina. Prilikom DFS obilaska datog usmerenog grafa \(G\) implicitno se formira DFS drvo, odnosno DFS šuma. Jednostavnosti radi, možemo pretpostaviti da se DFS šuma sastoji od jednog drveta. Naime, svako drvo DFS šume se može analizirati zasebno, jer je jasno da su čvorovi svake komponente jake povezanosti podskup čvorova nekog pojedinačnog drveta u DFS šumi. Alternativno, kao što je objašnjeno u poglavlju 2.3.1.2, graf možemo proširiti novim čvorom \(v\) ulaznog stepena 0 koji je povezan granama sa svim ostalim čvorovima. Prošireni graf sem komponenti grafa \(G\) ima samo još jednu dodatnu jednočlanu komponentu jake povezanosti \(\{v\}\). Naime, nijedan drugi čvor ne može biti sa njim u komponenti jake povezanosti, jer je ulazni stepen čvora \(v\) jednak \(0\).
U narednom razmatranju ćemo u potpunosti zanemariti direktne grane (one grane koje spajaju pretke sa potomcima). Naime, od svakog pretka do potomka se već može stići granama DFS drveta, pa se uklanjanjem direktnih grana ne menja dostižnost čvorova i komponente jake povezanosti ostaju nepromenjene.
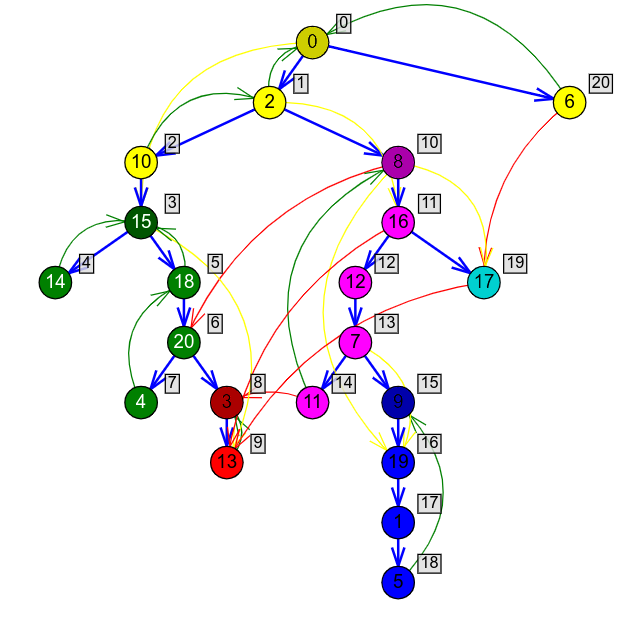
Razmotrimo graf prikazan na slici 3. Komponente jake povezanosti su obeležene raznim bojama. Zapaža se da su čvorovi svake komponente jake povezanosti grupisani u DFS drvetu, tj. da je svaka komponenta deo nekog poddrveta DFS drveta. U dosta slučajeva čvorovi čak imaju i uzastopne redne brojeve, mada to ne mora biti uvek slučaj (na primer, poslednji čvor žute komponente se otkriva tek nakon što se otkriju i obrade sve ostale komponente). Ovaj odnos položaja komponenti unutar DFS drveta je ključan element Tardžanovog algoritma i u nastavku ćemo se potruditi da ga preciznije ispitamo i formalno dokažemo njegova svojstva.
Pre toga probajte da na prethodnom apletu prikažete DFS drvo i da samostalno na nekoliko primera probate da odredite komponente na DFS drvetu (približavanjem čvorova drveta koji su u istoj komponenti).
Prilikom DFS obilaska važno nam je da znamo kada smo prešli iz jedne komponente u drugu. U svaku komponentu ulazimo tako što najpre posetimo njen čvor koji ima najmanji redni broj (dolazni DFS broj). Nazovimo baznim čvorom \(b\) (engl. base vertex) komponente \(X\) onaj čvor te komponente koji ima najmanji redni broj pri dolaznoj DFS numeraciji, tj. onaj čvor \(b \in X\) za koji važi \(b.\mathit{Pre}=\min_{v\in X} v.\mathit{Pre}\).
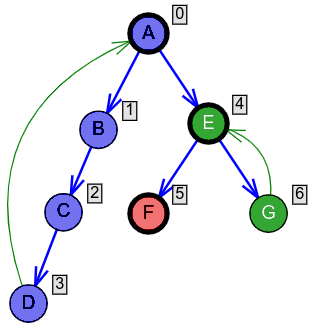
Primer 2.6.2. Razmotrimo graf sa slike 4: on sadrži tri komponente jake povezanosti: \(\{A,B,C,D\}\), \(\{E,G\}\) i \(\{F\}\). Bazni čvor prve komponente je čvor \(A\), druge \(E\), a treće \(F\).
Bazni čvorovi grafa sa slike 3 su \(0, 15, 3, 8, 9\) i \(17\).
Naredni primer će nam ukazati na važne odnose koji u svakoj komponenti važe između njenog baznog čvora i ostalih čvorova. Te odnose ćemo zatim formalizovati i dokazati u lemi 2.6.1.
Primer 2.6.3. U primerima na slikama 3 i 4 zapaža se da su svi čvorovi svake komponente potomci njenog baznog čvora u DFS drvetu. Dodatno, na putu od baznog čvora do bilo kog drugog čvora u toj komponenti kroz grane DFS drveta ne može da bude prekida, tj. put sadrži samo čvorove te komponente. Na primer, u grafu prikazanom na slici 4 jednoj komponenti povezanosti pripadaju čvorovi \(\{A,B,C,D\}\) i čvorovi \(B\), \(C\) i \(D\) jesu potomci baznog čvora te komponente – čvora \(A\) u DFS drvetu. Slično važi i za čvor \(G\) koji je potomak baznog čvora \(E\) svoje komponente. Posebno, s obzirom da čvorovi \(A\) i \(D\) pripadaju istoj, prvoj komponenti jake povezanosti grafa, to važi i za čvorove \(B\) i \(C\) koji se nalaze na putu od čvora \(A\) do čvora \(D\) kroz grane DFS drveta. Naredna lema dokazuje da to nije slučajno. Istaknimo i da obratno ne mora da važi, tj. jasno je da mogu postojati potomci baznog čvora u DFS drvetu koji ne pripadaju njegovoj komponenti: na primer, čvorovi \(E\), \(F\) i \(G\) grafa sa slike 4 su potomci čvora \(A\), ali se ne nalaze sa njim u istoj komponenti.
Naredna lema pokazuje da zapažanja iz primera 2.6.3 važe i u opštem slučaju.
Lema 2.6.1. [Odnos baznih i ostalih čvorova komponente] Neka je \(b\) bazni čvor komponente \(X\). Tada:
Dokaz. Pretpostavimo suprotno, odnosno da u komponenti \(X\) postoje čvorovi koji nisu u poddrvetu \(T_b\) DFS drveta sa korenom u \(b\), i neka je \(v\) jedan od takvih čvorova. Neka je \((v_0=b, v_1,\ldots,v_k=v)\) put od \(b\) do \(v\) kroz čvorove komponente \(X\). Neka je \(v_{i}\) prvi čvor na tom putu koji nije u poddrvetu \(T_b\) (dakle, čvor \(b\) je predak čvorova \(v_j\) za \(j=1,\ldots,i-1\)). Tada je grana \((v_{i-1},v_i)\) poprečna u odnosu na DFS drvo. Naime, pošto \(v_i\) nije u poddrvetu \(T_b\), grana \((v_{i-1},v_i)\) nije grana DFS drveta, a ne može biti ni povratna, jer bi onda čvor \(v_i\) bio predak čvora \(b\) i \(b\) ne bi bio bazni čvor te komponente. Sve poprečne grane u odnosu na DFS drvo su usmerene ulevo, pa i grana \((v_{i-1},v_i)\). Dakle, čvor \(v_i\) je levo od čvora \(v_{i-1}\), pa važi \(v_i.\mathit{Pre} < v_{i-1}.\mathit{Pre}\). Dodatno, oni imaju zajedničkog pretka \(z\) u DFS drvetu (slika 5, levo).
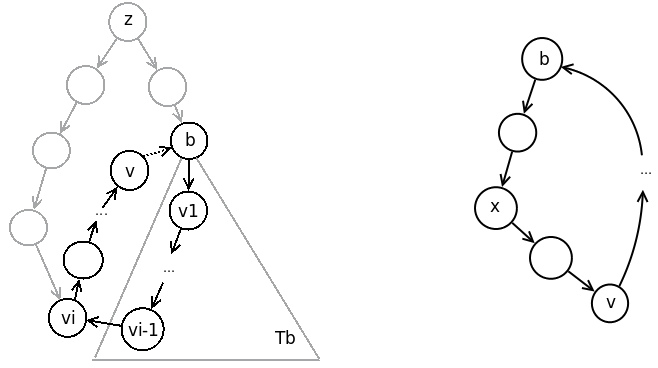
Čvor \(z\) ne može biti jedan od čvorova \(v_0=b, v_1, v_2, \ldots, v_{i-1}\), jer bi inače čvor \(v_i\) bio u poddrvetu sa korenom u čvoru \(b\). Pošto je \(b\) predak čvora \(v_{i-1}\), onda je \(z\) i zajednički predak čvorova \(v_i\) i \(b\), te je čvor \(v_i\) levo i od čvora \(b\), pa važi \(v_i.\mathit{Pre} < b.\mathit{Pre}\). Pritom, čvor \(v_i\) pripada komponenti u kojoj je bazni čvor \(b\), jer je obostrano dostižan sa čvorom \(b\): \(b\) je dostižan iz čvora \(v_i\) putem od \(v_i\) do \(v_k=v\) i dalje putem od \(v_k\) do \(b\) koji postoji jer je \(v\), po pretpostavci, u ovoj komponenti. Ovo je u suprotnosti sa pretpostavkom da je \(b\) bazni čvor ove komponente. Dakle, svi čvorovi komponente \(X\) se nalaze u poddrvetu \(T_b\) DFS drveta.
Dokažimo drugi deo leme. Neka je \(x\) proizvoljni čvor na putu od \(b\) do \(v\) (slika 5, desno). Postoji put od čvora \(b\) do čvora \(x\) kroz grane DFS drveta, a takođe i put od čvora \(x\) do čvora \(b\): taj put dobija se nadovezivanjem puta od \(x\) do \(v\) kroz grane DFS drveta i puta od \(v\) do \(b\) (ovaj put postoji jer čvorovi \(v\) i \(b\) pripadaju istoj komponenti). Stoga je \(x\) u istoj komponenti kao i čvor \(b\). Zaključujemo da svi čvorovi na putu od čvora \(b\) do čvora \(v\) kroz grane DFS drveta pripadaju komponenti čiji je bazni čvor \(b\). \(\Box\)
Naredni primer sugeriše činjenicu da se čvorovi svake komponente dobijaju tako što se iz poddrveta čiji je koren bazni čvor te komponente uklone druge komponente. Ovo ćemo formalizovati i dokazati u lemi 2.6.2.
Primer 2.6.4. Na slikama 3 i 4 zapaža se da se svi čvorovi koji pripadaju bilo kojoj komponenti jake povezanosti dobijaju tako što se iz drveta čiji je koren bazni čvor te komponente uklone poddrveta čiji su korenovi bazni čvorovi drugih komponenti. Na primer, ako na slici 3 iz drveta čiji je koren čvor \(0\), odsečemo poddrveta čiji su koreni čvorovi \(15\) i \(8\) ostaju samo žuti čvorovi koji čine jednu komponentu. Proverite da ovo važi i za sve ostale komponente.
U grafu prikazanom na slici 4 čvor \(A\) je bazni čvor. Čvorovi \(E\) i \(F\) su takođe bazni čvorovi i pritom su potomci baznog čvora \(A\). Primetimo da su čvorovi koji pripadaju komponenti čiji je bazni čvor \(A\) oni koji su potomci od \(A\), a nisu potomci ni čvora \(E\) ni čvora \(F\): to su čvorovi \(B\), \(C\) i \(D\). Slično, čvorovi koji pripadaju komponenti sa baznim čvorom \(E\) su oni koji su potomci od \(E\), a nisu potomci od \(F\), što je samo čvor \(G\).
Naredna lema dokazuje da zapažanja iz primera 2.6.4 važe u opštem slučaju.
Lema 2.6.2. [Odsecanje drugih komponenti] Neka je \(b\) bazni čvor neke komponente i neka su \(b_1, b_2,\ldots, b_k\) bazni čvorovi nekih drugih komponenti koji su potomci čvora \(b\) u odnosu na DFS drvo. Tada se komponenta kojoj pripada čvor \(b\) sastoji od svih potomaka čvora \(b\) koji nisu potomci nekog od čvorova \(b_1,b_2,\ldots,b_k\).
Dokaz. Neka je čvor \(v\) u istoj komponenti kao i čvor \(b\). Na osnovu leme 2.6.1 on mora biti potomak u odnosu na DFS drvo čvora \(b\). Pretpostavimo suprotno tvrđenju, da je on potomak i čvora čvora \(b_i\) za neko \(i\), \(1\le i \le k\) (slika 6).
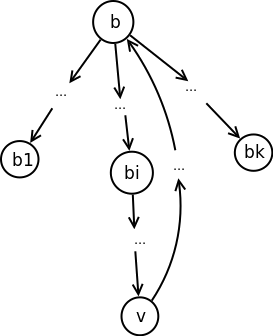
Pošto je \(b_i\) potomak čvora \(b\), onda postoji put kroz grane DFS drveta od čvora \(b\) do čvora \(b_i\). Slično, pošto je čvor \(v\) potomak čvora \(b_i\) postoji put od čvora \(b_i\) do čvora \(v\), a zbog toga što su \(v\) i \(b\) u istoj komponenti, postoji i put od čvora \(v\) do čvora \(b\). Nadovezivanjem ova dva puta dobija se put od čvora \(b_i\) do \(b\). Na osnovu toga što je čvor \(b\) dostižan iz čvora \(b_i\) i čvor \(b_i\) dostižan iz čvora \(b\) sledi da su čvorovi \(b\) i \(b_i\) u istoj komponenti što je u suprotnosti sa pretpostavkom leme jer su \(b\) i \(b_i\) bazni čvorovi različitih komponenti. Dakle, čvorovi koji su u istoj komponenti kao i čvor \(b\) ne mogu biti potomci i nekog drugog baznog čvora \(b_i\), koji je potomak čvora \(b\). \(\Box\)
Pod pretpostavkom da nekako umemo da odredimo bazne čvorove svih komponenti jake povezanosti (što je problem kojim ćemo se pozabaviti u poglavlju 2.6.2.3), leme 2.6.1 i 2.6.2 nam daju mogućnost da odredimo koji su čvorovi zajedno sa nekim baznim čvorom u istoj komponenti jake povezanosti. I više od toga, ovakav raspored komponenata nam daje mogućnost da ih prilično jednostavno nabrojimo tokom DFS obilaska.
Potrebno je da u neku pogodnu strukturu podataka smeštamo čvorove u redosledu DFS obilaska, a da neposredno pre nego što napustimo neki čvor proverimo da li je on bazni i ako jeste ispišemo (i uklonimo) njega i sve njegove potomke koji se i dalje nalaze u toj strukturi podataka: to će biti čvorovi koji su nakon njega posećeni, i nakon njega dodati u tu strukturu. Dakle, elemente treba dodavati na kraj ove strukture podataka i uklanjati ih sa kraja ove strukture. Struktura podataka koju je pogodno koristiti u ove svrhe je stek. Naime, prilikom označavanja čvora \(v\) u toku DFS obilaska, čvor \(v\) se upisuje na zaseban namenski stek namenjen nabrajanju komponenata jake povezanosti. Kada se završi poziv algoritma DFS iz čvora \(v\), u sklopu izlazne obrade, ako je \(v\) bazni čvor neke komponente, sa steka se uklanja čvor \(v\) i svi čvorovi iznad njega na steku (naravno, unazad: od elementa na vrhu steka pa sve do čvora \(v\)). Na taj način ako je čvor \(v\) bazni, izdvaja se komponenta koja sadrži čvor \(v\) i svi njeni čvorovi uklanjaju se sa steka. Redosled uklanjanja baznih čvorova nam garantuje da ćemo sa baznim čvorovima neke komponente ukloniti samo one potomke koji nisu potomci nekog drugog baznog čvora. Opisani postupak prikazan je u algoritmu 3.
\begin{algorithm}
\caption{Izdvajanje komponenti jake povezanosti uz pomoć steka}
\begin{algorithmic}
\Procedure{DFS}{početni čvor $u$}
\State{označi čvor $u$}
\State{stavi čvor $u$ na stek}
\ForAll{čvor $v$ koji je sused čvora $u$}
\If{čvor $v$ nije označen}
\State{}
\Call{DFS}{$v$}
\EndIf
\EndFor
\If{čvor $u$ je bazni čvor komponente}
\State{skidaj elemente sa steka sve dok se ne skine $u$}
\State{skinuti čvorovi su svi čvorovi komponente čiji je bazni čvor $u$}
\EndIf
\EndProcedure
\State{}
\ForAll{neoznačen čvor $u$}
\State{}
\Call{DFS}{$u$}
\EndFor
\end{algorithmic}
\end{algorithm}
U narednom apletu možete videti kako prethodno opisani algoritam funkcioniše. Bazni čvorovi svake komponente su podebljani. Prilikom ulazne DFS obrade čvora prikazuje se njegov ulazni DFS broj, a prilikom izlazne obrade prikazuje se i njegov izlazni DFS broj. Prilikom ulazne obrade čvor se stavlja na namenski stek. U trenutku izlazne obrade baznog čvora cela njegova komponenta je obrađena i nalazi se na vrhu steka, pa se sa steka skidaju elementi sve dok se on ne skine.
Dokažimo korektnost ovog algoritma.
Teorema 2.6.1. [Korektnost nabrajanja komponenti pomoću steka] Za svaki bazni čvor \(b\) komponente jake povezanosti grafa \(G\) važi sledeće:
Pri ulaznoj obradi čvora \(b\), on se postavlja na stek.
Pre njegove izlazne obrade ispravno su obrađene sve komponente jake povezanosti u poddrvetu čiji je on koren. Na vrhu steka, iznad čvora \(b\), nalaze se svi čvorovi njegove komponente povezanosti.
Nakon izlazne obrade čvora \(b\) on se uklanja sa steka, zajedno sa svim čvorovima njegove komponente, nakon čega je sadržaj steka isti kao pri ulazu u čvor \(b\).
Dokaz. Dokaz se može izvesti indukcijom po broju \(m\) komponenti jake povezanosti koje čine graf.
Za \(m=1\), postoji samo jedan bazni čvor \(b\) i on je koren celog DFS drveta. U prvom koraku DFS obrade on se postavlja na prazan stek, zatim se svi ostali čvorovi, jedan po jedan stavljaju na stek, sve dok se na samom kraju DFS obilaska ne dođe do izlazne obrade čvora \(b\). U tom trenutku (pošto je on jedini bazni čvor), svi čvorovi se skidaju sa steka, obrađuje se ispravno jedina komponenta grafa i stek na kraju ostaje prazan, kao što je i bio pre ulaska u čvor \(b\).
Neka je tvrđenje tačno za grafove sa manje od \(m\) komponenti i neka je \(G\) graf sa \(m\) komponenti. Neka je \(b\) prvi bazni čvor na koji se nailazi pri DFS obilasku (to je čvor iz kog pokrećemo DFS obilazak), a neka su \(b_1, b_2,\ldots, b_{m-1}\) njegovi potomci, koji su bazni čvorovi ostalih komponenti. Svaki od njih će tokom DFS obilaska iz čvora \(b\) u nekom trenutku biti stavljen na stek. Prema induktivnoj hipotezi, posle završetka DFS obilaska iz čvora \(b_i\), \(1\le i\le m-1\), izdvojene su sve komponente dostižne iz čvora \(b_i\) i svi njihovi čvorovi su uklonjeni su sa steka, ostavljajući stek svaki put u stanju kao pre ulaza u čvor \(b_i\). To znači da se u trenutku izlazne obrade čvora \(b\) na steku nalaze svi čvorovi drveta sa korenom \(b\) (potomci čvora \(b\)), koji ne pripadaju ni jednom drvetu čiji je koren neki od čvorova \(b_1, \ldots, b_{m-1}\). Međutim, na osnovu leme 2.6.2 znamo da su to tačno čvorovi komponente čiji je bazni čvor \(b\). Prilikom izlazne obrade čvora \(b\) ta komponenta se ispravno izdvaja, njeni čvorovi se skidaju sa steka i stek ostaje prazan. \(\Box\)
Da bi Tardžanov algoritam bio kompletan, nedostaje još samo da formulišemo neki efektivni test kojim bismo mogli da za dati čvor ispitamo da li je on bazni čvor svoje komponente.
U svakoj komponenti jake povezanosti moguće je stići od bilo kog čvora do bilo kog drugog čvora. Zato se od svakog čvora komponente može stići do njenog baznog čvora, što je “najniži” tj. čvor sa najmanjim rednim brojem u toj komponenti. Poželjno je zato da za svaki čvor ispitamo koji je “najniži” čvor do kog se može stići u drvetu, u nadi da će to uvek biti bazni čvor komponente.
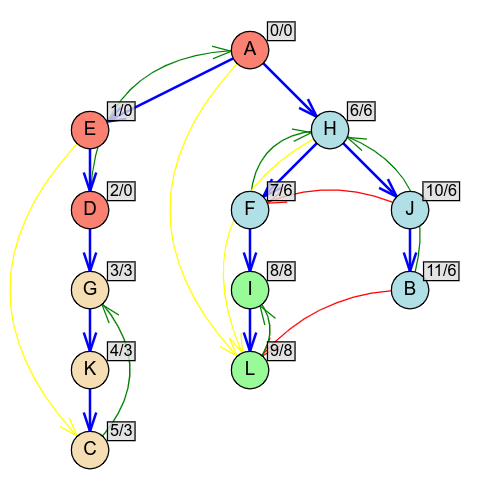
Razmotrimo graf na slici 7. Vidimo da je na ovom grafu nastupila idealna situacija, jer je “najniži” čvor do kog je moguće vratiti se iz proizvoljnog čvora grafa uvek bazni čvor komponente kojoj taj čvor pripada. Bazni čvorovi se onda lako prepoznaju tako što su to oni čvorovi kojima se redni broj poklapa sa najmanjim brojem čvora do kog se iz tog čvora možemo vratiti.
Ipak, problem nije tako jednostavan, jer ponekad poprečne grane mogu da nas odvedu do čvora koji ima manji redni broj od rednog broja baznog čvora komponente. Razmotrimo sada graf na slici 8. Zbog poprečne grane \((F,B)\) se iz čvora \(F\) (redni broj \(5\)) možemo vratiti do čvora \(B\) (redni broj \(4\)), pa zatim do čvora \(I\) (redni broj \(2\)). Dakle, najmanji redni broj čvora do koga možemo da se vratimo iz čvora \(F\) (redni broj \(5\)) je \(2\), pa, pošto taj broj nije jednak rednom broju čvora \(F\), čvor \(F\) ne prepoznajemo kao bazni čvor komponente, a on to jeste. Dakle, razmatranje poprečne grane \((F,B)\) pokazuje da jednostavan kriterijum koji smo formulisali nije sasvim korektan. S druge strane, ako se poprečna grana \((D,J)\) ne bi gledala, ne bi bilo moguće ustanoviti da se iz čvora \(D\) (redni broj \(8\)) možemo vratiti do čvora \(J\) (redni broj \(7\)), pa zatim unazad do čvora \(F\) (redni broj \(5\)), i ne bi bilo jasno da čvor \(D\) pripada komponenti čiji je bazni čvor \(F\).
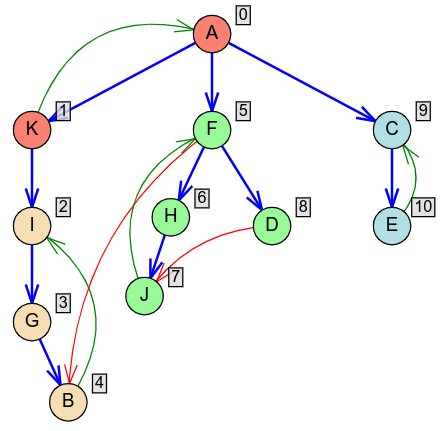
Jasno je da moramo modifikovati kriterijum tako da uključi razmatranje nekih, a isključi razmatranje nekih drugih poprečnih grana. Vidimo da ne treba određivati najmanji redni broj proizvoljnog čvora do kog se možemo “spustiti” iz datog čvora \(v\), jer taj čvor može da bude takav da ne pripada istoj komponenti kojoj pripada i čvor \(v\). Nas zapravo zanima da za svaki čvor \(v\) odredimo najmanji broj čvora u njegovoj komponenti do kog je moguće vratiti se. Lako se može dokazati da je čvor bazni čvor komponente ako i samo ako se taj broj poklapa sa njegovim rednim brojem. Direktne grane, već smo konstatovali, nemaju nikakvog uticaja na određivanje ovog broja. Dopušteno je “podizati se” granama drveta, a “spuštati se” povratnim granama (jer povratne grane uvek spajaju dva čvora koja su u istoj komponenti, pošto kreiraju ciklus sa granama drveta između ta dva čvora) i “spuštati se” poprečnim granama (ka čvorovima sa manjim rednim brojevima), ali ne svim poprečnim granama, već samo onim koje spajaju čvorove koji su u istoj komponenti (poprečna grana može povezivati dva čvora iz iste ili iz različite komponente, slika 8).
Iako deluje da smo problem određivanja svih čvorova neke komponente sveli na problem određivanja njenog baznog čvora komponente, a problem određivanja baznog čvora komponente na poznavanje čvorova komponente, videćemo uskoro da nismo napravili cirkularnu definiciju i da smo se približili rešenju problema.
Opisani brojevi (najmanji redni broj čvora unutar komponente do kog se možemo popeti) daju jasan kriterijum za određivanje baznih čvorova, ali se ne mogu jednostavno odrediti korišćenjem jednog DFS obilaska (što je ilustrovano primerom 2.6.5). Umesto njih, koriste se redni brojevi čvorova unutar komponente, ali do kojih se može stići samo kretanjem niz grane drveta, a zatim povratkom uz najviše jednu poprečnu ili povratnu granu. Za svaki čvor određujemo “najniži” čvor njegove komponente dostižan jednom povratnom ili poprečnom granom. Redni broj tog čvora ponovo obeležavamo sa \(L(v)\) (engl. lowlink), kao u poglavlju 2.5, ali jasno je da \(L(v)\) mora biti definisan nešto drugačije nego u slučaju neusmerenih grafova. Neka je \(X\) komponenta koja sadrži čvor \(v\). Označimo sa \(M\) najmanji redni broj čvora komponente \(X\) do koga se iz čvora \(v\) može stići putem koji se sastoji od grana DFS drveta i koji se završava najviše jednom povratnom ili poprečnom granom. Vrednost \(L(v)\) definišemo kao \(\min\{v.\mathit{Pre}, M\}\), odnosno:
\[L(v)=\min\{v.\mathit{Pre},\min_{\substack{w\in X\\\mathrm{postoji\ grana\ }(t,w),\ t\in T_v\\(t,w)\mathrm{\ je\ poprecna\ ili\ povratna}}} w.\mathit{Pre}\}.\]
Na slici 9 prikazan je graf sa slike 4, pri čemu je uz svaki čvor \(v\), pored rednog broja u dolaznoj numeraciji, prikazana i vrednost \(L(v)\) čvora. Bazni čvorovi su tačno oni čvorovi za koje važi \(v.Pre=L(v)\).
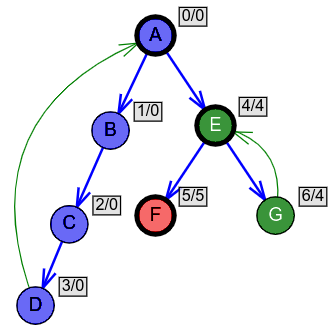
U narednom apletu možete proveriti svoje razumevanje funkcije \(L\) tj. najnižeg čvora dostižnog unutar komponente dostižnog povratnom ili poprečnom granom.
Primer 2.6.5. Graf na slici 10 ima jednu komponentu i na njemu se može videti kako se “najniži” čvor u komponenti do kog se može doći može odrediti praćenjem lanca putanja određenog vrednostima funkcije \(L\).
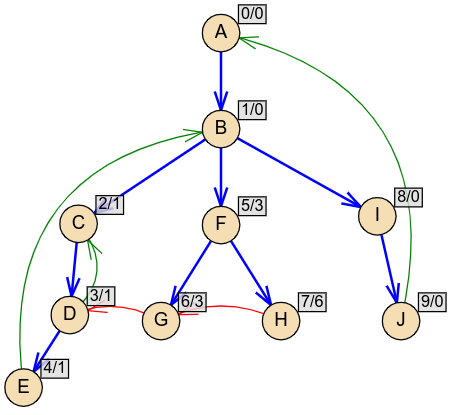
Na primer,
\(L(F)=3\), jer se od čvora \(F\) granom drveta stiže do \(G\), pa zatim poprečnom granom do čvora \(D\) koji ima redni broj 3. Dakle, iz drveta sa korenom \(F\) se jednom poprečnom granom vraćamo u drvo sa korenom \(D\).
\(L(D)=1\), jer se od čvora \(D\) granom drveta stiže do čvora \(E\), pa zatim povratnom granom do čvora \(B\) koji ima redni broj 1. Dakle iz drveta sa korenom \(D\) se jednom povratnom granom vraćamo u drvo sa korenom \(B\).
\(L(B)=0\), jer se od čvora \(B\) granama drveta redom stiže do čvorova \(I\), pa zatim \(J\), a onda se povratnom granom od \(J\) vraćamo u čvor \(A\) koji ima redni broj \(0\). Dakle, iz drveta sa korenom \(B\) se jednom povratnom granom možemo vratiti u bazni čvor \(A\) sa rednim brojem \(0\).
Da bi se za čvor \(F\) ustanovilo da se može vratiti u čvor \(A\) sa rednim brojem \(0\) potrebno je, između ostalog, da vidimo granu \((J,A)\), što se dešava tek pred kraj DFS obilaska, nakon što je obilazak čvora \(F\) završen. Ovo ukazuje na to da je za određivanje najnižeg čvora u komponenti do kog se može stići (što je uvek bazni čvor) potrebno više puta obilaziti graf. Videćemo da to nije slučaj sa vrednostima \(L(v)\) i da se one mogu lako odrediti tokom jedinog obilaska grafa koji vrši Tardžanov algoritam.
Analogno lemi 2.5.2, moguće je formulisati lemu koja opisuje rekurzivne veze između vrednosti funkcije \(L\) između čvorova DFS drveta (na osnovu koje sledi postupak za određivanje vrednosti funkcije \(L\) tokom DFS obilaska).
Bilo koji čvor koji nije bazni ima manju vrednost \(L(v)\) od svog rednog broja \(v.\mathit{Pre}\). Zaista, postoji put od njega do baznog čvora, koji u nekom trenutku mora da “pobegne” iz poddrveta sa korenom \(v\), bilo povratnom granom bilo poprečnom granom ka čvoru u istoj komponenti i da nas dovede do čvora sa manjim rednim brojem. Prateći lanac ovakvih putanja, doći ćemo u jednom trenutku i do baznog čvora za koji je \(L(v) = v.\mathit{Pre}\). Dokažimo ovo i formalno.
Lema 2.6.3. Čvor \(v\) je bazni čvor ako i samo ako važi \(L(v)=v.\mathit{Pre}\).
Dokaz. Pokažimo prvi smer tvrđenja: ako je čvor \(v\) bazni onda važi \(L(v)=v.\mathit{Pre}\). Pretpostavimo suprotno, odnosno da za bazni čvor \(v\) važi \(L(v) < v.\mathit{Pre}\) i pokažimo da onda čvor \(v\) nije bazni čvor. Prema definiciji vrednosti \(L\), postoji čvor \(w\) u istoj komponenti kao i \(v\) takav da je \(L(v)=w.\mathit{Pre}\). Stoga je \(w.\mathit{Pre} < v.\mathit{Pre}\) te čvor \(v\) nije bazni čvor.
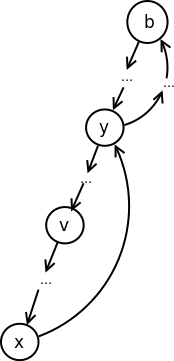
Dokažimo sada suprotni smer implikacije: ako za čvor \(v\) važi uslov \(L(v)=v.\mathit{Pre}\), onda je čvor \(v\) bazni. Pretpostavimo suprotno: da važi uslov \(L(v)=v.\mathit{Pre}\), a da čvor \(v\) nije bazni čvor. Neka je \(b\) bazni čvor komponente koja sadrži čvor \(v\). Prema lemi 2.6.1 čvor \(b\) je predak čvora \(v\). Pošto su \(b\) i \(v\) u istoj komponenti, postoji prosti put \(p\) od \(v\) do \(b\). Neka je \(y\) prvi čvor na putu \(p\) koji nije u poddrvetu sa korenom u \(v\) i neka je \(x\) čvor koji mu prethodi na putu \(p\):
ako je grana \((x,y)\) povratna (slika 11), onda je \(y\) predak čvora \(v\) i \(L(v) \le y.Pre < v.Pre\), suprotno pretpostavci (čvor \(y\) nije na putu od \(v\) do \(x\), jer je put \(p\) po pretpostavci prost);
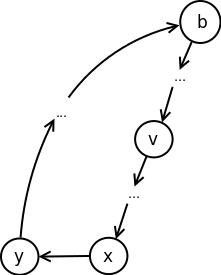
ako je grana \((x,y)\) poprečna (slika 12), onda je ona usmerena ulevo i \(y.\mathit{Pre} < x.\mathit{Pre}\). S obzirom na to da su poddrvo sa korenom u \(y\) i poddrvo sa korenom u \(v\) disjunktni i da postoji grana od potomka čvora \(v\) (odnosno \(x\)) do \(y\), na osnovu svojstava poprečnih grana možemo zaključiti da važi \(y.\mathit{Pre} < v.\mathit{Pre}\). Odavde sledi da je \(L(v) \le y.\mathit{Pre}\), jer je \(y\) u istoj komponenti jake povezanosti kao i \(v\) i dostižan je preko niza grana DFS drveta nakon koga sledi jedna povratna ili poprečna grana. Na osnovu ovoga i činjenice da je \(y.\mathit{Pre} < v.\mathit{Pre}\), dobijamo da važi \(L(v) < v.\mathit{Pre}\), suprotno pretpostavci.
\(\Box\)
Finalizujmo opis algoritma tako što ćemo prikazati kako se određuju vrednosti \(L(v)\). Prilikom ulaska u čvor \(u\) tokom DFS obilaska dodeljujemo mu redni broj \(v.\mathit{Pre}\) i inicijalizujemo \(L(v) = v.\mathit{Pre}\). Zatim obrađujemo sve grane \((v, w)\) koje vode iz čvora \(v\) do nekog čvora \(w\).
Ako čvor \(w\) nije posećen, rekurzivno vršimo njegov obilazak i grana \((v, w)\) postaje grana DFS drveta. Nakon rekurzivnog poziva poznata je vrednost \(L(w)\), pa vrednost \(L(v)\) ažuriramo na vrednost \(\min\{L(v), L(w)\}\).
Ako je čvor \(w\) posećen, a grana \((v,w)\) je povratna ili poprečna, a čvor \(v\) je u istoj komponenti, analiziramo i ažuriramo vrednost \(L(v)\) na vrednost \(\min\{L(v), w.\mathit{Pre}\}\) – ovo je u skladu sa definicijom vrednosti \(L\), i ne koristi se izraz \(\min\{L(v), L(w)\}\) jer je dopušten prelaz preko proizvoljno mnogo grana drveta, ali samo preko jedne povratne ili poprečne grane.
Ako je čvor \(w\) posećen, a grana \((v,w)\) je direktna ili je poprečna, a čvor \(w\) je u nekoj drugoj komponenti, ovu granu prosto preskačemo.
Ostaje pitanje kako efikasno utvrditi da li poprečna grana \((v, w)\) grana vodi ka čvoru iste ili druge komponente povezanosti. Jedno rešenje je da se primeti da se ono može svesti na pitanje da li se u trenutku obrade ove grane njen krajnji čvor \(w\) nalazi u namenskom steku namenjenom nabrajanju komponenti ili ne. Dajmo prvo malo precizniju karakterizaciju elemenata koji se nalaze na steku.
Lema 2.6.4. [Čvorovi koji ostaju na steku nakon izlazne obrade] Čvor se nalazi na steku nakon njegove izlazne obrade ako i samo ako postoji put u grafu od njega do nekog čvora koji se trenutno nalazi ispod njega na steku
Dokaz. Ako bi se na steku nalazio čvor tokom čije je izlazne obrade utvrđeno da se u grafu ne može od tog čvora doći do nekog čvora ispod njega na steku, taj čvor bi bio bazni čvor komponente i morao bi prilikom svoje izlazne obrade biti uklonjen sa steka zajedno sa ostalim čvorovima njegove komponente. \(\Box\)
Primer 2.6.6. U grafu na slici 8 se u trenutku ulazne obrade čvora \(F\) na steku nalaze čvorovi \(A\) i \(K\) pri čemu je završena izlazna obrada samo čvora \(K\). On se nalazi na steku jer postoji put od njega do čvora \(A\) koji je ispod njega na steku.
Sada možemo dokazati i karakterizaciju poprečnih grana.
Lema 2.6.5. [Poprečne grane i stek] Poprečna grana \((v, w)\) vodi iz čvora \(v\) ka čvoru \(w\) koji je u trenutku obrade čvora \(v\) na steku ako i samo ako su \(v\) i \(w\) u istoj komponenti povezanosti.
Dokaz. Ako je grana \((v, w)\) poprečna, čvor \(w\) je levo od \(v\). On će kao takav biti posećen pre čvora \(v\) i pritom dodat na stek, a u trenutku posete čvora \(v\) njegova izlazna obrada će već biti završena.
Ako čvor \(w\) nije više na steku prilikom obrade čvora \(v\), on je morao biti uklonjen sa steka zajedno sa svim čvorovima svoje komponente, što znači da nije u istoj komponenti sa \(v\).
Ako je čvor \(w\) i dalje na steku prilikom obrade čvora \(v\), na osnovu leme 2.6.4, prateći lanac putanja ka sve nižim i nižim čvorovima na steku, iz njega ćemo se “spustiti” do nekog zajedničkog pretka čvorova \(v\) i \(w\), čime se obezbeđuje da su čvorovi \(v\) i \(w\) uzajamno dostižni i nalaze se u istoj komponenti. \(\Box\)
Primer 2.6.7. U grafu na slici 8 poprečna grana \(FB\) vodi ka čvoru \(B\) koji se ne nalazi više na steku u trenutku obrade čvora \(F\), pa \(F\) i \(B\) nisu u istoj komponenti. Poprečna grana \(DJ\) vodi ka čvoru \(J\) koji je i dalje na steku u trenutku obrade čvora \(D\), pa su čvorovi \(D\) i \(J\) u istoj komponenti.
Dakle, važi sledeće:
poprečna grana \((v, w)\) vodi ka čvoru \(w\) koji je u trenutku obrade čvora \(v\) na steku ako i samo su \(v\) i \(w\) u istoj komponenti povezanosti;
povratna grana \((v, w)\), jasno, uvek vodi ka čvoru \(w\) koji je u trenutku obrade čvora \(v\) na steku (jer je \(w\) predak od \(v\), pa je završena njegova ulazna obrada tokom koje je je stavljen na stek, ali nije završena njegova izlazna obrada niti izlazna obrada baznog čvora njegove komponente, pa \(w\) nije još mogao biti skinut sa steka);
ako direktna grana \((v, w)\) vodi ka čvoru \(w\) na steku, važi da je \(w.\mathit{Pre} > v.\mathit{Pre}\), pa ta grana ne može uticati na vrednost \(L(v)\).
Zato u kodu možemo proveravati one grane \((v, w)\) koje vode od čvora \(v\) do čvora \(w\) koji se nalazi na steku, ne analizirajući posebno njihovu vrstu.
Ispitivanje da li je čvor na steku prolaskom kroz stek nije efikasno, pa dodatno koristimo namenski niz u kome ćemo tokom izvršavanja algoritma pamtiti za svaki čvor da li se trenutno nalazi na steku ili ne. Alternativno rešenje je da se prilikom skidanja čvora \(v\) sa steka njegove vrednosti \(v.\mathit{Pre}\) i \(L(v)\) postave na \(+\infty\). Kada se to uradi sve poprečne grane mogu biti posećene, ali do smanjenja vrednosti \(L(v)\) može doći samo kod grana ka čvorovima koji su još na steku i nalaze se u istoj komponenti.
Sada možemo dati i zaokruženi pseudokod Tardžanovog algoritma.
\begin{algorithm}
\caption{Tardžanov algoritam za određivanje komponenata jake povezanosti}
\begin{algorithmic}
\Procedure{DFS}{čvor $v$}
\State{dodeli redni broj $v.Pre$}
\State{$L(v) = v.Pre$}
\State{stavi $v$ na stek}
\ForAll{sused $w$ čvora $v$}
\If{čvor $w$ nije označen}
\State{}
\Call{DFS}{$w$}
\State{$L(v) = \min\{L(v), L(w)\}$}
\ElsIf{$w$ je na steku}
\State{$L(v) = \min\{L(v), \Pre{w}\}$}
\EndIf
\EndFor
\If{$L(v) = \Pre{v}$}
\State{skidaj elemente sa steka sve dok se ne skine $v$}
\State{skinuti čvorovi su svi čvorovi komponente sa korenom $v$}
\EndIf
\EndProcedure
\ForAll{neoznačen čvor $v$}
\State{}
\Call{DFS}{$v$}
\EndFor
\end{algorithmic}
\end{algorithm}
Tardžanov algoritam za određivanje komponenti jake povezanosti oslanja se na DFS obilazak grafa, te je složenosti \(O(|V|+|E|)\).
Algoritam se može implementirati u jeziku C++ na sledeći način.
int vreme_dolazna = 1;
void dfsTarjan(int cvor, vector<int> &dolazna, vector<int> &lowlink,
stack<int> &redosledUObilasku, vector<bool> &naSteku,
vector<int>& komponente, int& komponenta) {
dolazna[cvor] = lowlink[cvor] = vreme_dolazna;
vreme_dolazna++;
redosledUObilasku.push(cvor);
naSteku[cvor] = true;
// rekurzivno prolazimo kroz sve susede koje nismo obisli
for (int sused : listaSuseda[cvor]) {
// ako cvor 'sused' do sada nismo posetili
if (dolazna[sused] == -1) {
// pokrecemo DFS obilazak iz cvora 'sused'
dfsTarjan(sused, dolazna, lowlink, redosledUObilasku, naSteku,
komponente, komponenta);
// ako je potrebno azuriramo vrednost L cvora 'cvor'
if (lowlink[sused] < lowlink[cvor])
lowlink[cvor] = lowlink[sused];
}
// ako je u pitanju povratna ili poprecna grana,
// azuriramo vrednost L za cvor 'cvor'
// samo ako se sused nalazi u steku
// to znaci da sused pripada istoj komponenti povezanosti
else if (naSteku[sused])
if (dolazna[sused] < lowlink[cvor])
lowlink[cvor] = dolazna[sused];
}
// ako je u pitanju bazni cvor komponente
// stampamo sve cvorove te komponente
if (dolazna[cvor] == lowlink[cvor]) {
while (true) {
// ispisujemo element sa vrha steka i uklanjamo ga
int cvor_komponente = redosledUObilasku.top();
komponente[cvor_komponente] = komponenta;
naSteku[cvor_komponente] = false;
redosledUObilasku.pop();
// ako smo stigli do baznog cvora prekidamo petlju
if (cvor_komponente == cvor)
break;
}
komponenta++;
}
}
// za svaki cvor odredjujemo redni broj komponente jake povezanosti
vector<int> tarjanSCC() {
int brojCvorova = listaSuseda.size();
vector<int> dolazna(brojCvorova, -1);
vector<int> lowlink(brojCvorova);
// stek na koji smestamo cvorove u redosledu DFS obilaska
stack<int> redosledUObilasku;
// vektor koji omogucava brzu proveru da li se cvor nalazi na steku
vector<bool> naSteku(brojCvorova, false);
// redni broj komponente svakog cvora
vector<int> komponente(brojCvorova, -1);
// redni broj tekuce komponente
int komponenta = 0;
// pokrecemo DFS iz svakog neposecenog cvora
for (int cvor = 0; cvor < brojCvorova; cvor++)
if (komponente[cvor] == -1)
dfsTarjan(cvor, dolazna, lowlink, redosledUObilasku, naSteku,
komponente, komponenta);
return komponente;
}#include <iostream>
#include <vector>
#include <string>
#include <stack>
using namespace std;
vector<vector<int>> listaSuseda;
int vreme_dolazna = 1;
void dfsTarjan(int cvor, vector<int> &dolazna, vector<int> &lowlink,
stack<int> &redosledUObilasku, vector<bool> &naSteku,
vector<int>& komponente, int& komponenta) {
dolazna[cvor] = lowlink[cvor] = vreme_dolazna;
vreme_dolazna++;
redosledUObilasku.push(cvor);
naSteku[cvor] = true;
// rekurzivno prolazimo kroz sve susede koje nismo obisli
for (int sused : listaSuseda[cvor]) {
// ako cvor 'sused' do sada nismo posetili
if (dolazna[sused] == -1) {
// pokrecemo DFS obilazak iz cvora 'sused'
dfsTarjan(sused, dolazna, lowlink, redosledUObilasku, naSteku,
komponente, komponenta);
// ako je potrebno azuriramo vrednost L cvora 'cvor'
if (lowlink[sused] < lowlink[cvor])
lowlink[cvor] = lowlink[sused];
}
// ako je u pitanju povratna ili poprecna grana,
// azuriramo vrednost L za cvor 'cvor'
// samo ako se sused nalazi u steku
// to znaci da sused pripada istoj komponenti povezanosti
else if (naSteku[sused])
if (dolazna[sused] < lowlink[cvor])
lowlink[cvor] = dolazna[sused];
}
// ako je u pitanju bazni cvor komponente
// stampamo sve cvorove te komponente
if (dolazna[cvor] == lowlink[cvor]) {
while (true) {
// ispisujemo element sa vrha steka i uklanjamo ga
int cvor_komponente = redosledUObilasku.top();
komponente[cvor_komponente] = komponenta;
naSteku[cvor_komponente] = false;
redosledUObilasku.pop();
// ako smo stigli do baznog cvora prekidamo petlju
if (cvor_komponente == cvor)
break;
}
komponenta++;
}
}
// za svaki cvor odredjujemo redni broj komponente jake povezanosti
vector<int> tarjanSCC() {
int brojCvorova = listaSuseda.size();
vector<int> dolazna(brojCvorova, -1);
vector<int> lowlink(brojCvorova);
// stek na koji smestamo cvorove u redosledu DFS obilaska
stack<int> redosledUObilasku;
// vektor koji omogucava brzu proveru da li se cvor nalazi na steku
vector<bool> naSteku(brojCvorova, false);
// redni broj komponente svakog cvora
vector<int> komponente(brojCvorova, -1);
// redni broj tekuce komponente
int komponenta = 0;
// pokrecemo DFS iz svakog neposecenog cvora
for (int cvor = 0; cvor < brojCvorova; cvor++)
if (komponente[cvor] == -1)
dfsTarjan(cvor, dolazna, lowlink, redosledUObilasku, naSteku,
komponente, komponenta);
return komponente;
}
int main() {
int brojCvorova, brojGrana;
cin >> brojCvorova >> brojGrana;
listaSuseda.resize(brojCvorova);
for (int i = 0; i < brojGrana; i++) {
string cvorOd, cvorDo;
cin >> cvorOd >> cvorDo;
listaSuseda[cvorOd[0] - 'A'].push_back(cvorDo[0] - 'A');
}
vector<int> komponente = tarjanSCC();
for (int k : komponente)
cout << k << endl;
return 0;
}Primer 2.6.8. Razmotrimo izvršavanje ovog algoritma na primeru grafa prikazanog na slici 13.
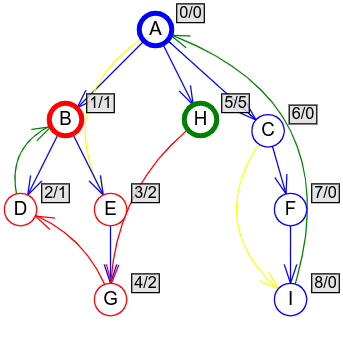
dfs(\(A\))
stek: \(A\)
inicijalizujemo \(A.\mathit{Pre} = L(A) = 0\)
grana \((A, B)\) postaje grana drveta
dfs(\(B\))
stek: \(A\), \(B\)
inicijalizujemo \(B.\mathit{Pre} = L(B) = 1\)
grana \((B, D)\) postaje grana drveta
dfs(\(D\))
stek: \(A\), \(B\), \(D\)
inicijalizujemo \(D.\mathit{Pre} = L(D) = 2\)
izlaz iz \(D\): \(L(D)=1\), a \(D.\mathit{Pre} = 2\), pa on nije bazni čvor komponente
\(L(B)\) nije veće od \(L(D)\), pa ostaje \(1\)
grana \((B, E)\) postaje grana drveta
dfs(\(E\))
stek: \(A\), \(B\), \(D\), \(E\)
inicijalizujemo \(E.\mathit{Pre} = L(E) = 3\)
grana \((E, G)\) postaje grana drveta
dfs(\(G\))
stek: \(A\), \(B\), \(D\), \(E\), \(G\)
\(E.\mathit{Pre} = L(E) = 4\)
izlaz iz \(G\): \(L(G) = 2\), a \(G.\mathit{Pre} = 4\), pa on nije bazni čvor komponente
\(L(E)\) smanjujemo na vrednost \(L(G) = 2\)
izlaz iz \(E\): \(L(E) = 2\), a \(E.\mathit{Pre} = 3\), pa on nije bazni čvor komponente
\(L(B)\) nije veće od \(L(E)\), pa ostaje \(1\)
izlaz iz \(B\): \(L(B) = B.\mathit{Pre} = 1\), on jeste bazni čvor komponente
sa steka se skidaju \(G\), \(E\), \(D\), \(B\) koji čine komponentu
stek: \(A\)
\(L(A)\) nije veće od \(L(B)\), pa ostaje \(0\)
direktna grana \((A, E)\) se preskače jer \(E\) nije na steku
grana \((A, H)\) postaje grana drveta
dfs(\(H\))
stek: \(A\), \(H\)
inicijalizujemo \(H.\mathit{Pre} = L(H) = 5\)
izlaz iz \(H\): \(L(H) = H.\mathit{Pre} = 5\), pa je on bazni čvor komponente
sa steka se skida: \(H\) koji čini komponentu
stek: \(A\)
\(L(A)\) nije veće od \(L(H)\), pa ostaje \(0\)
grana \((A, C)\) postaje grana drveta
dfs(\(C\))
stek: \(A\), \(C\)
inicijalizujemo \(C.\mathit{Pre} = L(C) = 6\)
grana \((C, F)\) postaje grana drveta
dfs(\(F\))
stek: \(A\), \(C\), \(F\)
inicijalizujemo \(F.\mathit{Pre} = L(F) = 7\)
grana \((F, I)\) postaje grana drveta
dfs(\(I\))
stek: \(A\), \(C\), \(F\), \(I\)
inicijalizujemo \(I.\mathit{Pre} = L(I) = 8\)
izlaz iz \(I\): \(L(I) = 0\), a \(I.\mathit{Pre} = 8\), pa on nije bazni čvor komponente
\(L(F)\) smanjujemo na vrednost \(L(I) = 0\)
izlaz iz \(F\): \(L(F) = 0\), a \(F.\mathit{Pre} = 7\), pa on nije bazni čvor komponente
\(L(C)\) smanjujemo na vrednost \(L(F) = 0\)
direktna grana \((C, I)\)
\(L(C)\) nije veće od \(L(I)\), pa ostaje \(0\)
izlaz iz \(C\): \(L(C) = 0\), a \(C.\mathit{Pre} = 6\), pa on nije bazni čvor komponente
\(L(A)\) nije veće od \(L(C)\), pa ostaje \(0\)
izlaz iz \(A\): \(L(A) = A.\mathit{Pre} = 0\), pa je on bazni čvor komponente
sa steka se skidaju: \(I\), \(F\), \(C\), \(A\), koji čine komponentu
stek:
U narednom apletu možete videti simulaciju rada kompletnog Tardžanovog algoritma, uključujući i računanje vrednosti \(L(v)\) za svaki čvor.
Još jedan algoritam linearne vremenske složenosti za određivanje komponenti jake povezanosti u usmerenom grafu je Kosaradžuov algoritam. Ovaj algoritam je osmislio (međutim nije publikovao) Kosaradžu (Rao Kosaraju) 1978. godine, a zatim je do njega kasnije nezavisno došao i Šarir (Micha Sharir) 1981. godine. On koristi dva DFS obilaska, pa je malo sporiji od Tardžanovog algoritma, ali je jednostavniji za razumevanje.
Primetimo da se prilikom izvršavanja Tardžanovog algoritma bazni čvorovi skidaju sa steka (zajedno sa ostalim čvorovima iz njihovih komponenata) u rastućem redosledu njihove odlazne numeracije. Pri tome, bazni čvor ima maksimalni redni broj odlazne DFS numeracije od svih čvorova svoje komponente. Obilazak baznih čvorova teče u obratnom topološkom redosledu čvorova kondenzovanog grafa (grafa dobijenog tako što se svaka komponenta predstavi samo njenim baznim čvorom), tj. obilazak tog acikličkog grafa se vrši od njegovih “listova” ka “korenu”.
Primer 2.6.9. 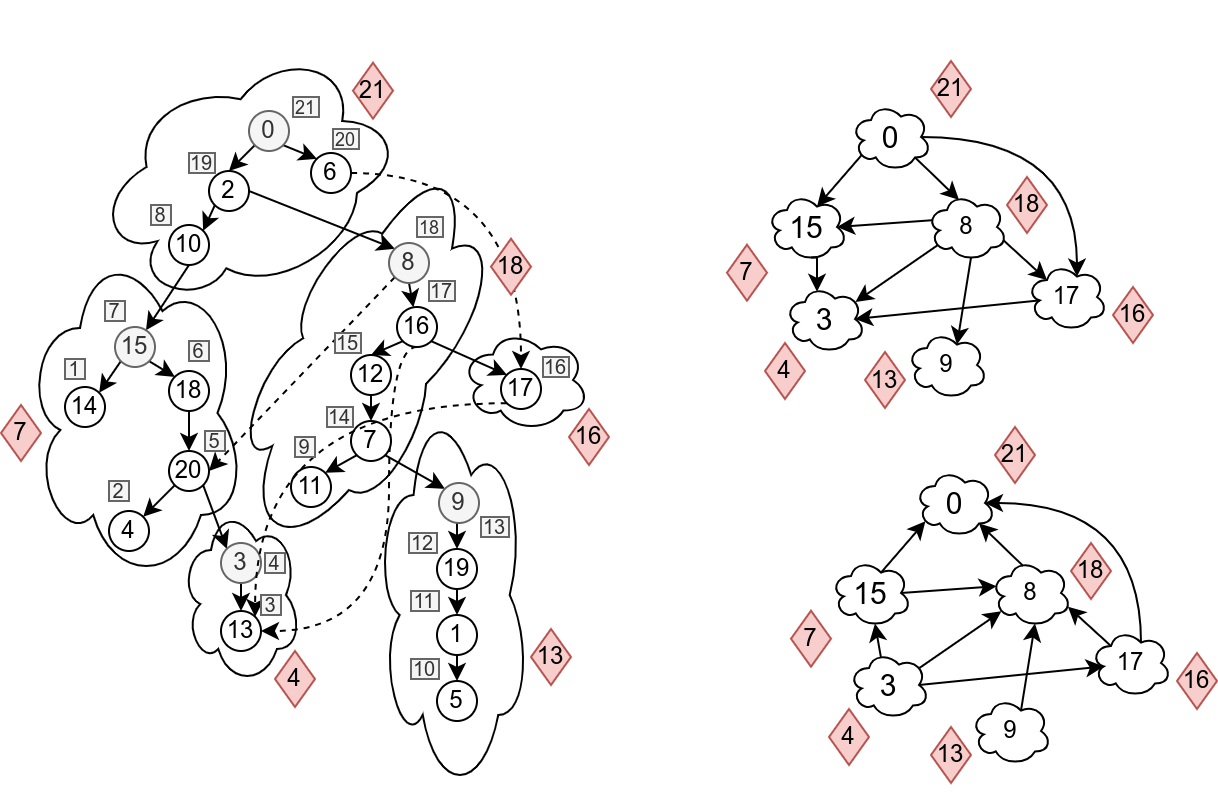
Na slici ?? prikazani su odlazni redni brojevi čvorova u DFS obilasku grafa sa slike 3. Jasno se vidi da bazni čvorovi imaju najveći odlazni broj od svih čvorova u njihovoj komponenti. Taržanov algoritam bi redom pronalazio komponente čiji su bazni čvorovi \(3\), \(15\), \(9\), \(17\), \(8\), i \(0\) (a njhovi odlazni redni brojevi su redom \(4\), \(7\), \(13\), \(16\), \(18\), \(21\)).
Možemo primetiti i da sve grane u kondenzovanom grafu vode od čvorova sa većim ka čvorovima sa manjim odlaznim brojevima. Dokažimo ovo i formalno. Označimo sa \(v.\mathit{Post}\) odlazni redni broj čvora \(v\) u nekom DFS obilasku koji po jednom posećuje sve čvorove grafa, a sa \(C.\mathit{Post}\) maksimalni odlazni redni broj svih čvorova komponente \(C\), tj. \(C.\mathit{Post}=\max_{v\in C} v.\mathit{Post}\).
Teorema 2.6.2. Neka su \(C\) i \(C'\) dve različite komponente jake povezanosti grafa \(G\) i neka u kondenzovanom grafu grafa \(G\) postoji grana \((C,C')\). Tada važi \(C.\mathit{Post}>C'.\mathit{Post}\).
Dokaz. Razlikujemo dva slučaja u odnosu na to koju od komponenti \(C\) i \(C'\) je algoritam DFS prvu posetio.
Pretpostavimo da DFS obilazak najpre posećuje neki čvor \(v\) komponente \(C\) i da u tom trenutku nijedan drugi čvor iz \(C\) i \(C'\) nije posećen. Svi čvorovi komponente \(C\) dostižni su iz čvora \(v\). Dodatno, s obzirom na to da u kondenzovanom grafu grafa \(G\) postoji grana \((C,C')\), iz čvora \(v\) su dostižni i svi čvorovi komponente \(C'\). To znači da će DFS obilazak pokrenut iz čvora \(v\) posetiti sve čvorove \(u\) iz \(C\cup C'\), te će oni biti njegovi potomci u DFS drvetu. Odatle sledi da je \(v.\mathit{Post}>u.\mathit{Post}\) za svako \(u\in C\cup C',\ u\neq v\), odakle važi \(C.\mathit{Post}>C'.\mathit{Post}\).
Pretpostavimo da DFS obilazak najpre posećuje neki čvor \(v\) komponente \(C'\) i da u tom trenutku nije posećen nijedan drugi čvor iz \(C'\) i \(C\). S obzirom na to da u kondenzovanom grafu grafa \(G\) postoji grana \((C,C')\) i da je kondenzovani graf aciklički, u kondenzovanom grafu ne sme postojati grana iz nekog čvora komponente \(C'\) ka nekom čvoru komponente \(C\). Stoga DFS obilazak pokrenut iz čvora \(v\) ne stiže ni do jednog čvora komponente \(C\). Odavde sledi da će čvorovi komponente \(C\) biti posećeni kasnije, odnosno važi \(C.\mathit{Post}>C'.\mathit{Post}\). \(\Box\)
Iz prethodne teoreme sledi da ako bismo DFS obilazak pokrenuli iz onog baznog čvora koji ima najmanji odlazni broj, sigurni bismo bili da bi taj DFS obilazak obišao sve čvorove u njegovoj komponenti i nijedan drugi čvor (jer u kondenzovanom grafu ne postoji nijedna grana koja bi mogla da “pobegne” iz te komponente). Međutim, mi taj bazni čvor ne znamo i nije nam lako da ga odredimo. Dakle, ako bismo vršili DFS obilazak od “listova” ka “korenu” kondenzovanog grafa, dobili bismo tačno jednu po jednu komponentu povezanosti, međutim, problem je što mi ne znamo čvorove koji pripadaju komponentama koje su “listovi” u kondenzovanom grafu i nije lako odrediti ih. Sa druge strane, sigurni smo da čvor sa najvećim odlaznim rednim brojem pripada “korenu”, tj. komponenti kondenzovanog grafa iz koje ne izlazi ni jedna grana. Ako bismo pokrenuli algoritam DFS iz tog čvora, nabrojali bismo i čvorove van te komponente, međutim, ne i ako grafu obrnemo grane!
Razmotrimo transponovani graf \(G^T\) grafa \(G\), dobijen promenom usmerenja svih grana u grafu: on ima iste komponente jake povezanosti kao i graf \(G\). Drugim rečima, dva čvora su uzajamno dostižna u polaznom grafu ako i samo ako su uzajamno dostižna u njemu transponovanom grafu. Zato, ako pokrenemo DFS obilazak iz bilo kog čvora u transponovanom grafu, sasvim smo sigurni da će u tom obilasku biti dostignuti svi čvorovi iz komponente jake povezanosti kojoj pripada polazni čvor (a možda i neki drugi). Primetimo da će kondenzovani grafovi grafova \(G\) i \(G^T\) biti međusobno transponovani (slika ??, desno). Drugim rečima, u transponovanom kondenzovanom grafu neće postojati grana iz korene komponente ka drugim komponentama. Stoga je za određivanje korene komponente koja sadrži neki čvor \(v\), dovoljno pokrenuti algoritam DFS iz čvora \(v\) u grafu \(G^T\). Na ovaj način se obilaze svi čvorovi komponente čvora \(v\) i ništa više od toga. Algoritam se dalje nastavlja po istom principu. Možemo iz grafa ukloniti sve ove čvorove (zapravo, označiti da su posećeni), pronaći čvor sa najvećom vrednošću odlazne numeracije u ostatku grafa, pokrenuti novi DFS obilazak u grafu \(G^T\) i tako dalje.
Odavde direktno sledi Kosaradžuov algoritam, koji ima dve faze:
u prvoj fazi se pokreće odgovarajući DFS obilazak grafa \(G\), sve dok se ne posete svi čvorovi grafa \(G\) (obilazak pokrećemo redom iz svakog čvora, pri čemu već posećene čvorove preskačemo); pritom se čvorovi grafa sortiraju rastuće prema vrednosti odlazne numeracije čvorova;
u drugoj fazi se konstruiše transponovani graf \(G^T\) grafa \(G\) i pokreneće niz DFS (ili BFS) obilazaka u redosledu dobijenom u prethodnom koraku, odnosno u opadajućem redosledu odlazne numeracije. Svaki skup čvorova, koji je dostižan u narednom obilasku daje novu komponentu jake povezanosti grafa \(G\).
Opisani algoritam se sastoji u pokretanju dva obilaska grafa, pa mu je vremenska složenost \(O(|V|+|E|)\).
Algoritam se u jeziku C++ može implementirati na sledeći način.
void odrediOdlazniRedosled(int cvor,
vector<bool>& posecen,
vector<int>& odlazniRedosled) {
posecen[cvor] = true;
for (int sused : listaSuseda[cvor])
if (!posecen[sused])
odrediOdlazniRedosled(sused, posecen, odlazniRedosled);
odlazniRedosled.push_back(cvor);
}
// za svaki cvor odredjuje se lista suseda
// iz kojih grane vode do tog cvora
vector<vector<int>> odrediTransponovaniGraf() {
vector<vector<int>> listaDolaznihSuseda;
int n = listaSuseda.size();
listaDolaznihSuseda.resize(n);
for (int cvor = 0; cvor < n; cvor++)
for (int sused : listaSuseda[cvor])
listaDolaznihSuseda[sused].push_back(cvor);
return listaDolaznihSuseda;
}
// dfs obilazkom iz datog cvora svim cvorovima dostiznim iz njega
// u transponovanom grafu se dodeljuje dati broj komponente
void odrediKomponentu(int cvor, vector<int>& komponente, int komponenta,
const vector<vector<int>>& listaDolaznihSuseda) {
komponente[cvor] = komponenta;
for (int sused : listaDolaznihSuseda[cvor])
if (komponente[sused] == -1)
odrediKomponentu(sused, komponente, komponenta,
listaDolaznihSuseda);
}
// za svaki cvor se odredjuje redni broj jake povezanosti
vector<int> kosarajuSCC() {
// vrsimo DFS i cvorove redjamo u niz u redosledu odlazne numeracije
int brojCvorova = listaSuseda.size();
vector<bool> posecen(brojCvorova, false);
vector<int> odlazniRedosled;
for (int cvor = 0; cvor < brojCvorova; cvor++)
if (!posecen[cvor])
odrediOdlazniRedosled(cvor, posecen, odlazniRedosled);
// odredjujemo transponovani graf
vector<vector<int>> listaDolaznihSuseda = odrediTransponovaniGraf();
// redni broj komponente svakog cvora
vector<int> komponente(brojCvorova, -1);
// redni broj tekuce komponente
int komponenta = 0;
// cvorove obilazimo u opadajucem redosledu odlazne numeracije
for (int i = brojCvorova - 1; i >= 0; i--) {
int cvor = odlazniRedosled[i];
// ako cvoru jos nije dodeljena komponenta
if (komponente[cvor] == -1)
// dodeljujemo komponentu njemu i svim cvorovima dostiznim
// iz njega u transponovanom grafu
odrediKomponentu(cvor, komponente, komponenta++,
listaDolaznihSuseda);
}
return komponente;
}#include <iostream>
#include <vector>
#include <string>
using namespace std;
vector<vector<int>> listaSuseda;
void odrediOdlazniRedosled(int cvor,
vector<bool>& posecen,
vector<int>& odlazniRedosled) {
posecen[cvor] = true;
for (int sused : listaSuseda[cvor])
if (!posecen[sused])
odrediOdlazniRedosled(sused, posecen, odlazniRedosled);
odlazniRedosled.push_back(cvor);
}
// za svaki cvor odredjuje se lista suseda
// iz kojih grane vode do tog cvora
vector<vector<int>> odrediTransponovaniGraf() {
vector<vector<int>> listaDolaznihSuseda;
int n = listaSuseda.size();
listaDolaznihSuseda.resize(n);
for (int cvor = 0; cvor < n; cvor++)
for (int sused : listaSuseda[cvor])
listaDolaznihSuseda[sused].push_back(cvor);
return listaDolaznihSuseda;
}
// dfs obilazkom iz datog cvora svim cvorovima dostiznim iz njega
// u transponovanom grafu se dodeljuje dati broj komponente
void odrediKomponentu(int cvor, vector<int>& komponente, int komponenta,
const vector<vector<int>>& listaDolaznihSuseda) {
komponente[cvor] = komponenta;
for (int sused : listaDolaznihSuseda[cvor])
if (komponente[sused] == -1)
odrediKomponentu(sused, komponente, komponenta,
listaDolaznihSuseda);
}
// za svaki cvor se odredjuje redni broj jake povezanosti
vector<int> kosarajuSCC() {
// vrsimo DFS i cvorove redjamo u niz u redosledu odlazne numeracije
int brojCvorova = listaSuseda.size();
vector<bool> posecen(brojCvorova, false);
vector<int> odlazniRedosled;
for (int cvor = 0; cvor < brojCvorova; cvor++)
if (!posecen[cvor])
odrediOdlazniRedosled(cvor, posecen, odlazniRedosled);
// odredjujemo transponovani graf
vector<vector<int>> listaDolaznihSuseda = odrediTransponovaniGraf();
// redni broj komponente svakog cvora
vector<int> komponente(brojCvorova, -1);
// redni broj tekuce komponente
int komponenta = 0;
// cvorove obilazimo u opadajucem redosledu odlazne numeracije
for (int i = brojCvorova - 1; i >= 0; i--) {
int cvor = odlazniRedosled[i];
// ako cvoru jos nije dodeljena komponenta
if (komponente[cvor] == -1)
// dodeljujemo komponentu njemu i svim cvorovima dostiznim
// iz njega u transponovanom grafu
odrediKomponentu(cvor, komponente, komponenta++,
listaDolaznihSuseda);
}
return komponente;
}
int main() {
int brojCvorova, brojGrana;
cin >> brojCvorova >> brojGrana;
listaSuseda.resize(brojCvorova);
for (int i = 0; i < brojGrana; i++) {
string cvorOd, cvorDo;
cin >> cvorOd >> cvorDo;
listaSuseda[cvorOd[0] - 'A'].push_back(cvorDo[0] - 'A');
}
vector<int> komponente = kosarajuSCC();
for (int k : komponente)
cout << k << endl;
return 0;
}Primer 2.6.10. U primeru na slici ?? pokretanjem DFS obilaska iz čvora \(0\) dobijaju se odlazni redni brojevi koji su prikazani na slici.
Primetimo da se u prvom koraku algoritma čvorovi uređuju u obrnutom topološkom redosledu grafa \(G\). Dodatno, algoritam generiše komponente jake povezanosti u opadajućem redosledu odlazne numeracije, odnosno čvorovi kondenzovanog grafa se dobijaju u topološkom redosledu.
Zadaci: