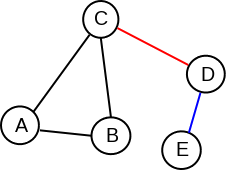
Primer 2.5.1. Ukoliko u grafu prikazanom na slici 1 uklonimo granu \((C,D)\) ili granu \((D,E)\) graf prestaje da bude povezan, te ove dve grane, svaka za sebe, čine most u datom grafu.
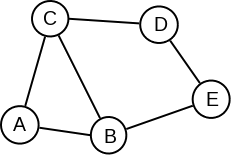
Postoje grafovi u kojima nema mostova (slika 2).
U ovom poglavlju bavićemo se pitanjem koliko je dati neusmereni graf dobro povezan. Drugim rečima interesuje nas da li u grafu postoji slaba tačka, odnosno usko grlo, čijim bi uklanjanjem graf prestao da bude povezan. U raznim praktičnim primenama ovaj problem je veoma značajan i potrebno je omogućiti da se uska grla u grafu brzo detektuju. Slična pitanja se mogu postaviti i za usmerene grafove, međutim, mi ćemo se u ovom poglavlju ograničiti na slučaj neusmerenih grafova.
Granu neusmerenog grafa \(G=(V,E)\) čijim se uklanjanjem iz grafa broj komponenti povezanosti grafa povećava nazivamo most (engl. bridge, cut edge). Specijalno, povezani graf nakon uklanjanja mosta prestaje da bude povezan.
U računarskim mrežama pronalaženje mostova može pomoći u identifikovanju kritičnih veza čiji kvar može dovesti do raspada mreže. U transportnim sistemima mostovi predstavljaju ključne rute koje povezuju različite oblasti, a čijim bi uklanjanjem transport bio onemogućen.
Primer 2.5.1. Ukoliko u grafu prikazanom na slici 1 uklonimo granu \((C,D)\) ili granu \((D,E)\) graf prestaje da bude povezan, te ove dve grane, svaka za sebe, čine most u datom grafu.

Postoje grafovi u kojima nema mostova (slika 2).

U narednom apletu možete proveriti svoje razumevanje pojma mostova.
Ukoliko u neusmerenom grafu \(G=(V,E)\) postoji čvor \(v\in V\) takav da se njegovim uklanjanjem iz grafa (zajedno sa granama koje su mu susedne) broj komponenti povezanosti grafa povećava, onda takav čvor nazivamo artikulacionom tačkom (engl. articulation point, cut vertex). Specijalno, povezani graf nakon uklanjanja artikulacione tačke prestaje da bude povezan.
U transportnim sistemima artikulacione tačke ukazuju na kritične raskrsnice čija bi eventualna nedostupnost (npr. u slučaju neke nesreće) imala značajan uticaj na tok saobraćaja. Na ovaj način mogu se planirati prioritetne investicije u saobraćajnu infrastrukturu. Slično, artikulacione tačke u električnim kolima predstavljaju komponente čijim bi otkazivanjem rada došlo do gubitka veze između ostalih komponenti. Identifikovanje ovih komponenti može poboljšati pouzdanost dizajna električnog kola. U kontekstu društvenih mreža artikulacione tačke predstavljaju osobe koje povezuju dve ili više različitih zajednica ljudi i čije bi uklanjanje razbilo mrežu na nepovezane grupe.
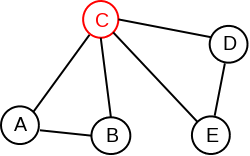
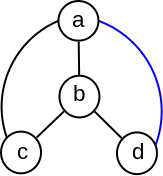
Primer 2.5.2. Ukoliko u povezanom grafu prikazanom na slici 3 uklonimo čvor \(C\), graf prestaje da bude povezan, te je čvor \(C\) jedna artikulaciona tačka ovog grafa. Štaviše, neposredno se proverava da je čvor \(C\) jedina artikulaciona tačka u ovom grafu.
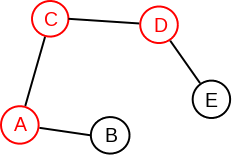
Graf može da ne sadrži artikulacione tačke (slika 2), a može i da sadrži veći broj artikulacionih tačaka (slika 4).
U narednom apletu možete proveriti svoje razumevanje pojma artikulacionih tačaka.
U nastavku ćemo razmotriti probleme pronalaženja svih mostova i artikulacionih tačaka u datom neusmerenom grafu. Bez smanjenja opštosti može se pretpostaviti da je dati graf povezan. Ako graf nije povezan, onda se mostovi i artikulacione tačke mogu tražiti nezavisno u svakoj komponenti povezanosti grafa.
Pozabavimo se najpre problemom određivanja mostova, za koji se pokazuje da je donekle jednostavniji.
Problem. Definisati algoritam koji u datom neusmerenom povezanom grafu određuje sve mostove.
Direktan način da se u datom neusmerenom povezanom grafu \(G=(V, E)\) pronađu svi mostovi podrazumeva da za svaku granu \(e\in E\) grafa \(G\) proverimo da li je graf bez grane \(e\) povezan (npr. korišćenjem algoritma DFS). Složenost ovog algoritma iznosi \(O(|E|\cdot(|V|+|E|))\).1
Postoji efikasniji algoritam za određivanje mostova u grafu. Mi ćemo u nastavku razmotriti algoritam koji je osmislio Robert Tardžan (engl. Robert Tarjan) i koji je linearne vremenske složenosti u funkciji veličini grafa.
Mostovi ne pripadaju ciklusima. Zaista, važi naredno trivijalno tvrđenje (koje navodimo bez dokaza).
Lema 2.5.1. [Veza mostova i ciklusa] Grana \((u,v)\) je most u grafu \(G\) ako i samo ako ne pripada nijednom ciklusu u grafu \(G\).
Specijalno, pošto u drvetu ne postoje ciklusi, ako je graf drvo, onda je svaka grana u tom grafu most (na primer, takav je graf na slici 4).
Razmotrimo DFS drvo dobijeno DFS obilaskom datog grafa \(G=(V,E)\). S obzirom na to da je polazni graf neusmeren, postoje dve vrste grana grafa u odnosu na DFS drvo: grane DFS drveta i grane koje povezuju potomka sa pretkom u odnosu na DFS drvo (u nastavku ćemo ih, jednostavnosti radi, zvati povratne grane, mada one nisu usmerene, pa se mogu istovremeno smatrati i za direktne i za povratne grane). Ako je grana \((u,v)\) povratna, ona ne može biti most u grafu, jer je deo ciklusa koji ta grana čini sa granama DFS drveta (videti primer na slici 5).
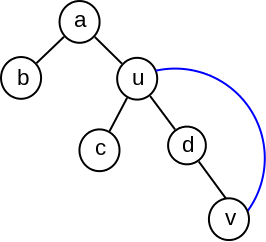
Dakle, mostovi mogu biti samo grane DFS drveta, te je dovoljno da algoritam razmatra samo njih kao kandidate, čime se može značajno smanjiti broj grana koje je potrebno proveravati. Međutim, ni ove grane ne moramo proveravati tehnikom grube sile. Neka je \((u,v)\) grana DFS drveta. Pretpostavimo da je DFS pretraga najpre posetila čvor \(u\) pa čvor \(v\), tj. da je čvor \(u\) roditelj čvora \(v\) u DFS drvetu grafa.
Za granu \((u,v)\) DFS drveta važi da je most ako i samo ako ne postoji ni jedna druga grana između nekog pretka čvora \(u\) (uključujući i čvor \(u\)) i nekog potomka čvora \(v\) (uključujući i čvor \(v\)).
Dakle, grana \((u, v)\) je most ako i samo ako poddrvo DFS drveta čiji je koren čvor \(v\) (koje je “iznad”2 čvora \(v\)) ostaje nepovezano sa delom grafa “ispod” ove grane tj. čvora \(u\). Drugim rečima tada ne postoji način da se stigne iz poddrveta \(T_v\) čiji je koren čvor \(v\) do čvora \(u\) ili nekog pretka čvora \(u\).
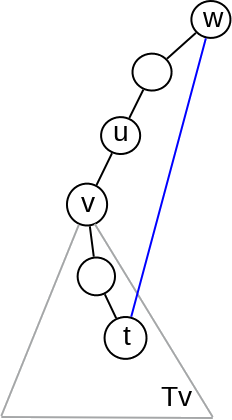
Potrebno je za svaki čvor \(v\in V\) izračunati koliko se “nisko” možemo vratiti nekom povratnom granom iz proizvoljnog čvora poddrveta \(T_v\) čiji je koren čvor \(v\). To možemo kvantifikovati na osnovu dolaznih DFS brojeva čvorova do kojih vode povratne grane iz \(T_v\) (“niži” čvorovi tj. čvorovi bliži korenu imaju i niže DFS brojeve). Kao što je ranije opisano, za svaki čvor \(v\in V\) može se odrediti vrednost \(v.\mathit{Pre}\) koja označava redni broj čvora \(v\) pri dolaznoj DFS numeraciji – tu vrednost ćemo u nastavku kraće zvati rednim brojem čvora \(v\). Cilj nam je da za svaki čvor \(v\) odredimo i redni broj “najnižeg” pretka dostižnog povratnom granom (engl. lowlink) do kog se možemo popeti nekom (najviše jednom) povratnom granom iz poddrveta \(T_v\) (slika 6). Naglasimo da ovo ne mora biti “najniži” dostižni predak, jer se uz korišćenje više povratnih grana možda može stići do nekog “nižeg” pretka tj. pretka koji ima manji DFS broj i bliže je korenu drveta.
Definišimo sada precizno pojam “najnižeg” pretka dostižnog povratnom granom3. Označimo sa \(L(v)\) (engl. lowlink) manju od vrednosti rednog broja čvora \(v\) i najmanje među vrednostima rednih brojeva čvorova do kojih se može stići povratnom granom iz proizvoljnog čvora poddrveta \(T_v\) (koje uključuje i čvor \(v\)), koja nije grana DFS drveta koja vodi od \(v\) ka njegovom roditeljskom čvoru u DFS drvetu. Moguće je da iz poddrveta \(T_v\) ne postoji nijedna grana ka pretku čvora \(v\) i tada je vrednost \(L(v)\) jednaka rednom broju čvora \(v\). Dakle važi sledeće:
\[L(v)=\min\{v.\mathit{Pre},\min_{\substack{w\mathrm{\ je\ predak\ }v \\ \mathrm{postoji\ grana\ }(t,w),\ t\in T_v, \\ \mathrm{\ koja\ ne\ spaja}\ v\ \mathrm{sa\ njegovim\ roditeljem}}} w.\mathit{Pre}\}.\]
Vrednost \(L(v)\) je definisana kao redni broj čvora, međutim, pošto postoji jasna bijekcija između čvorova i njihovih rednih brojeva možemo slobodno reći da je “najniži” predak čvora \(v\) dostižan povratnom granom onaj čvor čiji je redni broj \(L(v)\). Putanja od čvora \(v\) do njegovog “najnižeg” pretka dostižnog povratnom granom se uvek sastoji od niza grana DFS drveta za kojima sledi najviše jedna povratna grana. “Najniži” predak dostižan povratnom granom je uvek jedinstveno određen, ali putanja do njega ne mora biti (primer je dat na slici 7).
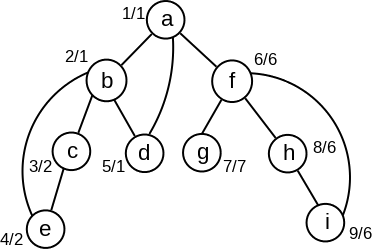
Primer 2.5.3. Na slici 8 dat je primer grafa gde je uz svaki čvor \(v\) prikazan njegov redni broj \(v.\mathit{Pre}\) i vrednost \(L(v)\). Na primer, važi \(L(c)=2\) i \(L(e)=2\) jer iz čvora \(e\) granom \((e,b)\) možemo stići do čvora \(b\) čija je redni broj jednak 2. Slično, važi \(L(b)=1\) jer iz čvora \(d\) koji je potomak čvora \(b\) možemo stići granom \((d,a)\) do čvora \(a\) čiji je redni broj 1.
U narednom apletu možete proveriti svoje razumevanje pojma “najnižeg” pretka dostižnog povratnom granom u neusmerenom grafu.
Sada možemo dati karakterizaciju mostova pomoću funkcije \(L\). Poddrvo \(T_v\) DFS drveta čiji je koren u čvoru \(v\) ostaće nakon izbacivanja grane \((u,v)\) nepovezano sa delom grafa “ispod” ove grane ako i samo ako važi \(L(v) > u.\mathit{Pre}\). Dakle, važi naredna teorema.
Teorema 2.5.1. [Karakterizacija mosta u grafu pomoću funkcije \(L\)] Grana \((u,v)\) je most u grafu \(G\) ako i samo ako važi \(L(v) > u.\mathit{Pre}\).
Primer 2.5.4. Razmotrimo graf prikazan na slici 9, levo.
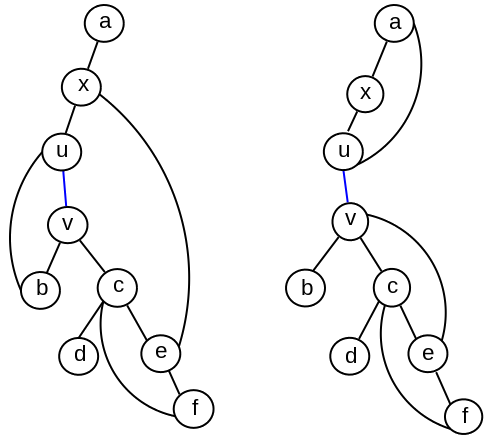
Grana \((u,v)\) nije most u grafu jer se iz poddrveta \(T_v\) možemo vratiti u deo DFS drveta “ispod” ove grane. Preciznije, iz čvora \(b\) možemo se vratiti u čvor \(u\), a iz čvora \(e\) u čvor \(x\). Pošto je čvor \(x\) “ispod” čvora \(u\), važi \(x.\mathit{Pre} < u.\mathit{Pre}\) i vrednost \(L(v)\) jednaka je rednom broju \(x.\mathit{Pre}\) čvora \(x\). Stoga nije zadovoljen uslov \(L(v) > u.\mathit{Pre}\), pa grana \((u, v)\) nije most. Čak i kad graf ne bi sadržao granu \((x,e)\), nakon izbacivanja grane \((u,v)\) mogli bismo se granom \((b,u)\) iz poddrveta \(T_v\) vratiti do čvora \(u\), a time i do proizvoljnog čvora “ispod” njega u DFS drvetu, te i u tom slučaju grana \((u,v)\) ne bi bila most u grafu (važilo bi da je \(L(v) = u.\mathit{Pre}\), pa ni tada ne bi važilo \(L(v) > u.\mathit{Pre}\)).
Razmotrimo sada graf sa slike 9, desno. Nakon izbacivanja grane \((u,v)\) iz grafa, iz poddrveta \(T_v\) možemo se vratiti “najniže” do čvora \(v\), tj. važi uslov \(L(v)=v.\mathit{Pre} > u.\mathit{Pre}\) i u ovom grafu grana \((u,v)\) jeste most.
Primetimo da, takođe, važi da je grana \((u,v)\) most ako i samo ako je \(L(v)=v\).
Ostaje pitanje kako efikasno izračunati vrednosti \(L(v)\) za sve čvorove \(v\) u grafu. Važi sledeća lema.
Lema 2.5.2. [Rekurzivna veza za \(L\)] Za svaki čvor \(v \in V\) neusmerenog grafa \(G = (V, E)\) važi:
\[L(v) = \min\{v.\mathit{Pre}, \min_{\substack{(v, w) \in E\\ w\ \mathrm{je\ predak\ cvora}\ v\\w\ \mathrm{nije\ roditelj\ cvora}\ v}} w.\mathit{Pre}, \min_{w\ \mathrm{je\ dete\ od}\ v} L(w)\}\](1)
Dokaz. Razmatrajmo proizvoljni čvor \(v\) i putanju od njega do “najnižeg” dostižnog čvora povratnom granom. Ta putanja je ili prazna ili se sastoji od tačno jedne povratne grane ili se sastoji od nekoliko grana DFS drveta za kojima sledi tačno jedna povratna grana. U jednakosti (1) se analiziraju sve moguće takve putanje i traži se ona najbolja.
Zaista, prazna putanja je obuhvaćena izrazom \(v.\mathit{Pre}\), a putanje koje se sastoje tačno od jedne povratne grane izrazom
\[\min_{\substack{(v, w)\in E\\ w \mathrm{\ je\ predak\ od}\ v\\w\ \mathrm{nije\ roditelj\ od}\ v}} w.\mathit{Pre}.\]
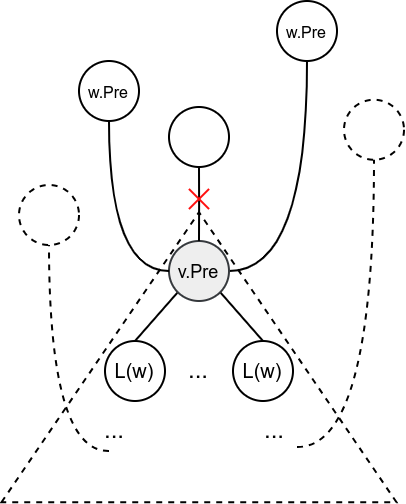
Ako putanja sadrži grane DFS drveta, nakon prelaska prve grane te putanje stiže se do nekog čvora \(w\) (koji nije roditelj čvora \(v\)), a zatim se nastavlja putanjom od čvora \(w\) do “najnižeg” dostižnog čvora povratnom granom krenuvši od čvora \(w\). Zaista, do svakog čvora dostižnog povratnom granom iz \(w\), može se stići putanjom i iz čvora \(v\) koja se završava povratnom granom, a ako bi se od čvora \(w\) moglo doći do nekog “nižeg” čvora putanjom sa povratnom granom, do njega bi se moglo stići putanjom sa povratnom granom i iz \(v\) (slika 10). Putanje od \(v\) koje sadrže bar jednu granu drveta se, dakle, analiziraju izrazom:
\[\min_{w\ \mathrm{je\ dete\ od}\ v} L(w).\]
\(\Box\)
Na osnovu ovoga, vrednosti funkcije \(L\) se mogu odrediti tokom DFS obilaska grafa. Definišemo rekurzivnu funkciju koja vrši DFS obilazak takvu da će nakon završetka njenog rekurzivnog poziva za proizvoljni čvor \(v\) grafa biti određene vrednosti \(v.\mathit{Pre}\) i \(L(v)\). Prilikom ulazne obrade čvora \(v\) dodeljuje mu se ulazni broj \(v.\mathit{Pre}\) i vrednost \(L(v)\) se inicijalizuje na tu vrednost. Nakon toga se obrađuju sve grane \((v, w)\). Prilikom obrade grane \((v, w)\), radi se sledeće:
Ako čvor \(w\) nije posećen, vrši se rekurzivno njegov obilazak i grana \((v, w)\) postaje grana DFS drveta. Nakon rekurzivnog poziva (u kom se vrši obrada kompletnog poddrveta čiji je koren \(w\)), izračunata je vrednost \(L(w)\), pa vrednost \(L(v)\) ažuriramo na vrednost \(\min\{L(v), L(w)\}\).
Ako je čvor \(w\) ranije posećen i nije roditelj čvora \(v\), ažuriramo vrednost \(L(v)\) na vrednost \(\min\{L(v), w.\mathit{Pre}\}\) (ovim se obrađuje svaka grana ka pretku \(w\) čvora \(v\), a ako je \(w\) posećeni potomak čvora \(v\), važi \(w.\mathit{Pre} > v.\mathit{Pre} \geq L(v)\), pa do ažuriranja neće doći).
Indukcijom, uz korišćenje leme 2.5.2, lako se može dokazati korektnost opisanog algoritma.
Teorema 2.5.2. [Korektnost algoritma izračunavanja funkcije \(L\)] Prethodnim algoritmom se ispravno izračunavaju vrednosti \(L(v)\) za sve čvorove \(v\).
Implementacija u nastavku određuje dolazne redne brojeve svih čvorova, redne brojeve njihovih “najnižih” predaka dostižnih povratnom granom tj. funkcije \(L\) i sve mostove u jednom DFS obilasku.
int vreme_dolazna = 0;
vector<bool> posecen;
vector<int> dolazna;
vector<int> lowlink;
vector<int> roditelj;
// niz grana koje su mostovi u grafu
vector<pair<int,int>> mostovi;
void dfs_mostovi(int cvor) {
// dodeljujemo redni broj cvoru 'cvor'
posecen[cvor] = true;
dolazna[cvor] = vreme_dolazna++;
// inicijalizujemo vrednost funkcije L cvora 'cvor' na njegov redni broj
lowlink[cvor] = dolazna[cvor];
// rekurzivno prolazimo kroz sve susede koje nismo obisli
for (int sused : listaSuseda[cvor]) {
// ukoliko je sused vec posecen
if (posecen[sused]) {
// ako grana ne vodi ka roditelju datog cvora
if (sused != roditelj[cvor])
// po potrebi azuriramo vrednost L cvora na redni broj suseda
if (dolazna[sused] < lowlink[cvor])
lowlink[cvor] = dolazna[sused];
} else {
// ukoliko sused nije posecen
// pamtimo granu DFS drveta
roditelj[sused] = cvor;
// pokrecemo pretragu iz cvora 'sused'
dfs_mostovi(sused);
// nakon obrade poddrveta čiji je koren cvor 'sused' vrednost L cvora 'sused' je odredjena;
// po potrebi azuriramo vrednost L za cvor 'cvor'
if (lowlink[sused] < lowlink[cvor])
lowlink[cvor] = lowlink[sused];
// proveravamo da li je grana (cvor, sused) most
// u ovom trenutku su vrednosti L cvora 'sused' i rednog broja cvora 'cvor' odredjene
if (lowlink[sused] > dolazna[cvor])
mostovi.emplace_back(cvor, sused);
}
}
}
void ispisi_mostove(int cvor) {
int brojCvorova = listaSuseda.size();
posecen.resize(brojCvorova, false);
dolazna.resize(brojCvorova);
lowlink.resize(brojCvorova);
roditelj.resize(brojCvorova, -1);
dfs_mostovi(cvor);
cout << "Mostovi u grafu su: ";
for (int i = 0; i < mostovi.size(); i++)
cout << "(" << mostovi[i].first << ", " << mostovi[i].second << ") " ;
cout << endl;
}Primer 2.5.5. U nastavku je ilustrovano izvršavanje opisanog algoritma na primeru jednostavnog neusmerenog grafa sa slike 11. Pretpostavlja se da je graf zadat listama povezanosti tako da su susedi svakog čvora uređeni leksikografski rastuće i da DFS pretraga započinje iz čvora \(a\).
Tardžanov algoritam za određivanje svih mostova u grafu se zasniva na DFS pretrazi, sa odgovarajućom dolaznom i odlaznom obradom koja je složenosti \(O(1)\), pa je vremenska složenost ovog algoritma \(O(|V|+|E|)\).
Pozabavimo se sada problemom određivanja artikulacionih tačaka.
Problem. Definisati algoritam koji u datom neusmerenom povezanom grafu određuje sve artikulacione tačke.
Artikulacione tačke u datom neusmerenom povezanom grafu možemo da odredimo tako što za svaki čvor \(v\in V\) grafa \(G\) izvršimo proveru da li je graf bez čvora \(v\) povezan. Složenost ovog direktnog algoritma je \(O(|V|\cdot(|V|+|E|))\). Umesto njega, razmotrićemo Tardžanov algoritam, koji je dosta efikasniji.
Veoma nalik Tardžanovom algoritmu za određivanje mostova je i algoritam za traženje artikulacionih tačaka u grafu. Pokušajmo da formulišemo kriterijum da je čvor artikulaciona tačka kroz nekoliko primera.
Primer 2.5.6. 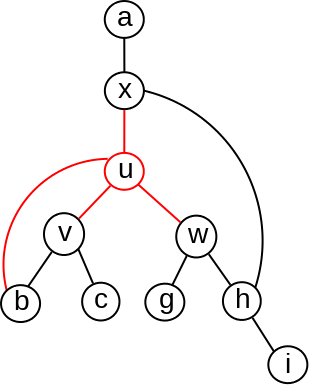
Razmotrimo graf sa slike ??. Čvor \(u\) ima dva deteta u DFS drvetu: \(v\) i \(w\). Nakon izbacivanja čvora \(u\) i njemu susednih grana iz grafa, iz poddrveta \(T_w\) možemo se vratiti u deo grafa “ispod” čvora \(u\) (jer je \(L(w)=x.\mathit{Pre}\)), međutim, iz poddrveta \(T_v\) možemo se vratiti “najniže” do čvora \(u\) (jer važi \(L(v)=u.\mathit{Pre}\)). S obzirom na to da čvor \(u\) ima dete \(v\) tako da nijedan čvor iz poddrveta \(T_v\) nije povezan sa nekim pretkom čvora \(u\), čvor \(u\) jeste artikulaciona tačka u grafu.
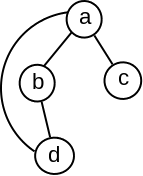
Primer 2.5.7. Primetimo da za koren \(a\) DFS drveta grafa sa slike 12 i njegovo dete \(b\) važi uslov \(L(b)=a.\mathit{Pre}\), tj. čvor \(a\) ima dete iz kojeg se ne možemo povratnom granom vratiti “niže” od čvora \(a\), a pritom čvor \(a\) nije artikulaciona tačka.
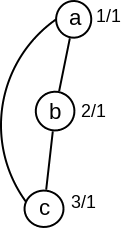
Razlog je to što je \(a\) koren DFS drveta, pa ne postoji deo DFS drveta “ispod” njega. Dakle, slučaj čvora koji je koren DFS drveta mora se zasebno razmatrati.
Primer 2.5.8. Razmotrimo graf sa slike 13.
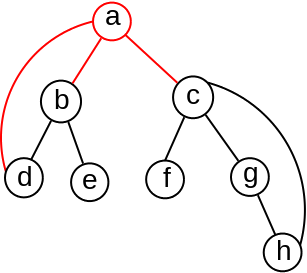
Čvor \(a\) kao koren DFS drveta ima dva deteta i nakon njegovog izbacivanja graf postaje nepovezan. Dakle, čvor \(a\) je artikulaciona tačka u grafu.
Karakterizacija artikulacionih tačaka data je narednom lemom.
Lema 2.5.3. [Karakterizacija artikulacionih tačaka] Čvor \(u\) je artikulaciona tačka grafa ako i samo ako je ispunjen jedan od naredna dva uslova:
Prvi uslov odgovara situaciji kada nakon izbacivanja čvora \(u\) iz grafa više nije moguće doći iz poddrveta \(T_v\) čiji je koren \(v\) dete čvora \(u\), do nekog pretka čvora \(u\). Ako je zadovoljen drugi uslov, s obzirom na to da u neusmerenim grafovima ne postoje poprečne grane, izbacivanje korena DFS drveta dovelo bi do “razbijanja” grafa na veći broj komponenti povezanosti (po jednu za svako dete korena DFS drveta).
Iz primera je jasno da se, kao i u slučaju mostova, za ispitivanje povezanosti elemenata poddrveta sa precima čvora mogu koristiti vrednosti \(L(v)\), čime se dobija naredna teorema.
Teorema 2.5.3. [Karakterizacija artikulacionih tačaka pomoću vrednosti funkcije \(L\)] Čvor \(u\) je artikulaciona tačka u grafu ako i samo ako važi jedan od naredna dva uslova:
U nastavku je data implementacija Tardžanovog algoritma kojim se u datom grafu određuju sve artikulacione tačke.
int vreme_dolazna = 0;
vector<bool> posecen;
vector<int> dolazna;
vector<int> lowlink;
vector<int> roditelj;
vector<bool> artikulacioneTacke;
void dfs_artikulacione(int cvor) {
// dodeljujemo redni broj cvoru 'cvor'
posecen[cvor] = true;
dolazna[cvor] = vreme_dolazna ++;
// broj dece cvora cvor
int broj_dece = 0;
// vrednost funkcije L za cvor 'cvor' inicijalizujemo na njegov redni broj
lowlink[cvor] = dolazna[cvor];
// rekurzivno prolazimo kroz sve susede koje nismo obisli
for (int sused : listaSuseda[cvor]) {
// ako je grana (cvor, sused) povratna i ne vodi ka roditelju cvora 'cvor'
if (posecen[sused]) {
if (sused != roditelj[cvor])
// po potrebi azuriramo vrednost L za cvor 'cvor'
if (dolazna[sused] < lowlink[cvor])
lowlink[cvor] = dolazna[sused];
} else {
// 'sused' je novo dete cvora 'cvor' u DFS drvetu
broj_dece++;
// dodajemo granu u DFS drvo
roditelj[sused] = cvor;
// pokrecemo pretragu iz cvora 'sused'
dfs_artikulacione(sused);
// nakon obrade poddrveta čiji je koren cvor 'sused' vrednost funkcije L
// cvora 'sused' je odredjena, pa po potrebi azuriramo vrednost L cvora 'cvor'
if (lowlink[sused] < lowlink[cvor])
lowlink[cvor] = lowlink[sused];
// ako 'cvor' nije koren DFS drveta i ako cvor nijedan cvor u poddrvetu cvora 'sused'
// nije povezan sa nekim pretkom cvora 'cvor' onda je 'cvor' artikulaciona tacka
if (roditelj[cvor] != -1 && lowlink[sused] >= dolazna[cvor])
artikulacioneTacke[cvor] = true;
}
}
// obradjena su sva deca cvora 'cvor'
// proveravamo da li je cvor 'cvor' koren DFS drveta i da li ima vise od jednog deteta
if (roditelj[cvor] == -1 && broj_dece > 1)
// ako je uslov ispunjen, cvor je artikulaciona tacka
artikulacioneTacke[cvor] = true;
}
void ispisi_artikulacione_tacke(int cvor) {
int brojCvorova = listaSuseda.size();
posecen.resize(brojCvorova, false);
dolazna.resize(brojCvorova);
lowlink.resize(brojCvorova);
roditelj.resize(brojCvorova, -1);
// inicijalno nijedan cvor nije artikulaciona tacka
artikulacioneTacke.resize(brojCvorova, false);
dfs_artikulacione(cvor);
cout << "Artikulacione tacke u grafu su: ";
for (int i = 0; i < artikulacioneTacke.size(); i++) {
if (artikulacioneTacke[i])
cout << i << " ";
}
cout << endl;
}Zadaci:
Primetimo da je uklanjanje grane iz grafa u slučaju kada je graf zadat listama povezanosti neefikasno, ali pošto se nakon uklanjanja svake grane izvršava algoritam pretrage u dubinu, ova operacija ne utiče na složenost kompletnog algoritma.↩︎
Pošto se drvo u ovom tekstu crta naopako, tako da mu je koren na vrhu crteža, a listovi na dnu, deo grafa “iznad” nekog čvora je nacrtan ispod tog čvora. U nastavku će biti korišćena terminologija u kojoj su termini iznad/ispod, niži/viži, gore/dole definisani u skladu sa položajem korena i listova, a ne u skladu sa naopakim crtanjem drveta. Ovo je u skladu i sa tim da je visina korena 0 i da visina čvorova raste kako se udaljavamo od korena. Da bismo smanjili mogućnost zabune, ove odrednice će biti pisane pod navodnicima.↩︎
Naglasimo da se pretpostavlja da se radi o neusmerenom grafu. U usmerenim grafovima je moguće definisati srodan pojam, ali je definicija komplikovanija i biće izložena u poglavlju 2.6.↩︎