Kada bunari ne bi postojali i kada bi samo bilo potrebe povezati sve kuće cevima, problem bi se direktno svodio na pronalaženje minimalnog povezujućeg drveta datog skupa kuća.
Mogućnost i potreba da se izgrade bunari naizgled čine zadatak komplikovanijim. Međutim, postoji veoma elegantan način da se i problem sa bunarima svede na problem minimalnog povezujućeg drveta, tj. da se izgradnja bunara modeluje izgradnjom cevi. Naime, svaki se bunar može zamisliti kao cev koja spaja kuću za zemljom u kojoj se već nalazi voda. Zato polazni graf u kome se nalaze kuće i cevi koje ih mogu povezati treba dopuniti jednim posebnim čvorom koji predstavlja zemlju i svaku kuću treba povezati sa tim čvorom pri čemu je cena cevi koja spaja zemlju i kuću jednaka ceni izgradnje bunara u toj kući. Kada se pronađe minimalno povezujuće drvo, ono će sigurno povezivati zemlju sa ostalim kućama, što znači da će voda iz zemlje sigurno moći da bude dopremljena do svake druge kuće (da bi zemlja bila povezana, sigurno će bar jedan bunar biti izgrađen). Ako gradimo usmeren graf, dovoljno je da usmerimo grane od zemlje ka svakoj kući (u zemlji se već nalazi voda, pa nije potrebno vraćati vodu iz neke kuće nazad do zemlje).
Kada se napravi ovako prošireni graf, minimalno povezujuće drvo može da se pronađe uobičajenim algoritmima.
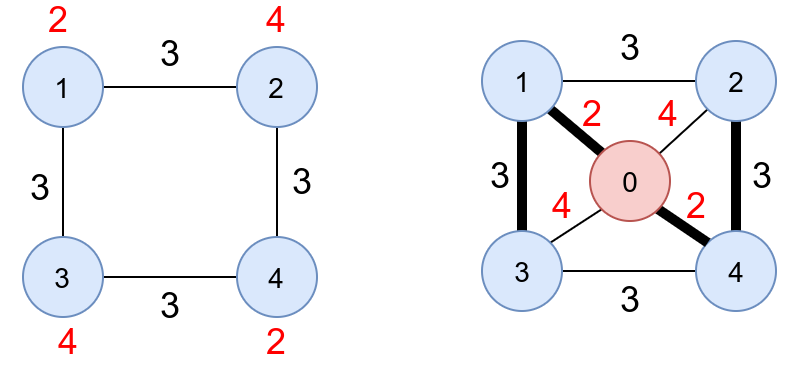
Primer 2.10.5. Na slici levo je prikazan graf gde su prikazane moguće cevi i cene bunara za svaku, dok je na slici desno prikazan proširen graf gde je uveden čvor \(0\) (zemlja) i bunari su predstavljeni cevima koje spajaju zemlju i kuće. Nacrtano minimalno povezujuće drvo ukazuje na to da je potrebno izgraditi bunare u kućama \(1\) i \(4\), a da je kuće \(2\) i \(3\) potrebno cevima povezati sa kućama \(1\) i \(4\).