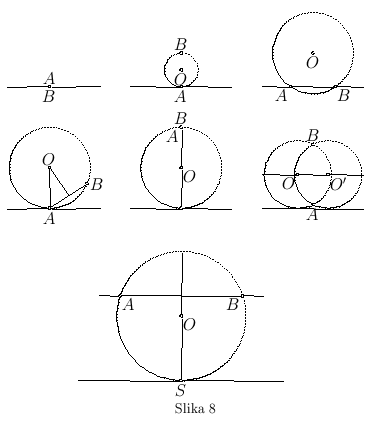Neka su date dve tačke A i B i prava  .
.
Treba kroz tačke A i B povući krug koji dodiruje pravu  .
.
- Analiza: Na simetrali s duži AB se nalazi centar svakog kruga koji prolazi kroz tačke A i B. Tačka S je presek simetrale s sa datom pravom
 .
.
Uzmimo na simetrali s proizvoljnu tačku K i spustimo normalu KD na pravu  . Pomoćni krug poluprečnika KD sa centrom u K dodiruje pravu
. Pomoćni krug poluprečnika KD sa centrom u K dodiruje pravu  , ali ne mora prolaziti kroz tačke A i B.
, ali ne mora prolaziti kroz tačke A i B.
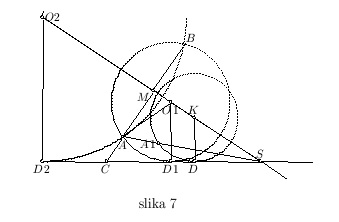
Neka prava AS seče krug K u tački 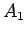 . Konstuišemo duž
. Konstuišemo duž 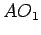 paralelno sa
paralelno sa 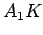 . Neka je
. Neka je 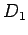 projekcija tačke
projekcija tačke 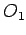 na pravu
na pravu  . Iz sledećih proporcija koje važe:
. Iz sledećih proporcija koje važe:
sledi da je
Kako je 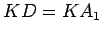 , to je
, to je 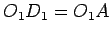 , a kako je tačka
, a kako je tačka 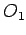 na simetrali s, to je
na simetrali s, to je 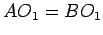 .
Dakle važi
.
Dakle važi
Za određivanje drugog traženog kruga O2 može se uzeti u obzir da je:
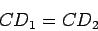 |
(1) |
gde je 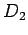 podnožje normale spuštene iz
podnožje normale spuštene iz 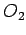 na pravu
na pravu  , a C, presek prave
, a C, presek prave  i prave kroz date tačke A i B. Jednačina (1) izražava jednakost potencije tačke C u odnosu na krug
i prave kroz date tačke A i B. Jednačina (1) izražava jednakost potencije tačke C u odnosu na krug 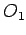 , čiji je izraz:
, čiji je izraz:
i potencije iste tačke C u odnosu na krug 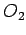
Posle određivanja tačke 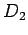 na
na  , konstrukcijom normale na
, konstrukcijom normale na  u tački
u tački 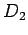 , određuje se položaj tačke
, određuje se položaj tačke 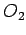 , centra drugog traženog kruga, a time i sam traženi krug.
, centra drugog traženog kruga, a time i sam traženi krug.
- Konstrukcija: Konstrukcija se vrši ovim redosledom:
- Za date tačke A, B i datu pravu
 se konstruiše simetrala s duži AB i presečna tačka te simetrale i prave
se konstruiše simetrala s duži AB i presečna tačka te simetrale i prave  se označi sa S. Na pravoj s uzme se proizvoljna tačka K i tačka M, sredšte duži AB.
se označi sa S. Na pravoj s uzme se proizvoljna tačka K i tačka M, sredšte duži AB.
- Iz tačke K spuštamo normalu na
 i podnožje označimo sa D. Krug sa poluprečnikom KD dodiruje pravu
i podnožje označimo sa D. Krug sa poluprečnikom KD dodiruje pravu  .
.
- Iz tačke A crtamo pravu AS i sa
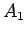 označimo presečnu tačku te prave sa krugom K.
označimo presečnu tačku te prave sa krugom K.
- Presek
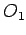 , prave
, prave 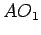 , paralelne sa
, paralelne sa 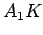 i simetrale s, određuje centar prvog traženog kruga.
i simetrale s, određuje centar prvog traženog kruga.
- Za drugi krug odmerimo od C duž
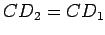 .
.
- Iz
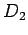 dižemo normalu na pravu
dižemo normalu na pravu  . Presek te normale sa simetralom s određuje centar
. Presek te normale sa simetralom s određuje centar 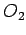 drugog traženog kruga.
drugog traženog kruga.
- Dokaz: U konstrukciji je postupno opisan način razmišljanja, tako da u dokazu navodimo samo stav da dve potencije iste tačke imaju iste vrednosti izražene pomoću kvadrata tangentnih odsečaka.
- Diskusija: Uslovi ovog zadatka se izražavaju položajem određene duži AB prema datoj pravoj
 . Za parametre tih podataka možemo uzeti ove tri veličine:
. Za parametre tih podataka možemo uzeti ove tri veličine:
- h je odstojanje tačke A od prave
 ,
,
- H je odstojanje tačke B od iste prave

- d je rastojanje između h i H
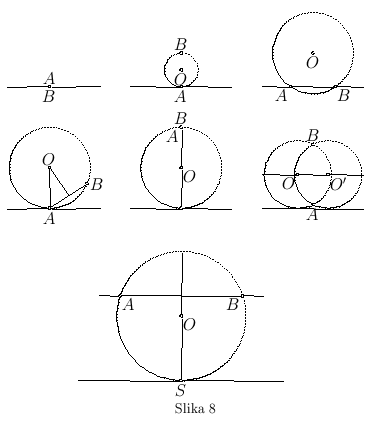
Pri tome, mora da važi:
Rezultati diskusije (sl. 8) mogu se svesti u tablicu:


2005-04-12
![]() .
.
![]() .
.