Neke osnovne primedbe
Uvedimo ovde radi boljeg razumevanja teksta nekoliko pojmova i teorema iz teorije krugova.
- Pojam potencije ili stepena tačke u odnosu na krug određuje se
proizvodom (sl.1)
gde su:
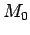 tačka čija se potencija određuje,
tačka čija se potencija određuje,
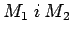 tačke na sečici kruga kroz
tačke na sečici kruga kroz 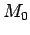 i
k kratka oznaka proizvoda dve duži: odsečka sečice
i
k kratka oznaka proizvoda dve duži: odsečka sečice 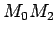 i spoljašnjeg dela
i spoljašnjeg dela 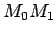 .
.
Ako sa T označimo dodirnu tačku tangente kruga povučene iz M0 možemo sastaviti proporciju
i, kao zaključak, izvesti ovaj rezultat:
koji izražava važnu teoremu:
Teorema 1
1.5
Potencija tačke u odnosu na krug jednaka je kvadratu odsečka tangente  povučene iz date tačke na krug.
povučene iz date tačke na krug.
k je pozitivno za tačku  van kruga; duži
van kruga; duži 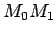 i
i 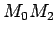 imaju isti smer.
imaju isti smer.
k je nula, ako je tačka 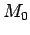 na periferiji kruga.
na periferiji kruga.
k je negativno, ako je tačka 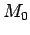 unutra u krugu;
unutra u krugu; 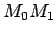 i
i 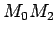 su suprotnih smerova.
su suprotnih smerova.
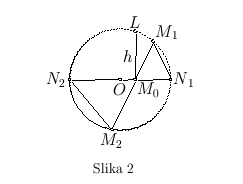
Za tačku 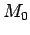 u krugu imamo(sl.2)
u krugu imamo(sl.2)
 gde su
gde su 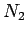 , O,
, O, 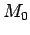 ,
, 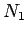 tačke na prečniku kruga, koji prolazi kroz tačku
tačke na prečniku kruga, koji prolazi kroz tačku 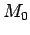 . Trouglovi
. Trouglovi 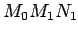 i
i 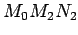 su slični.
su slični.
Ako stavimo 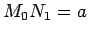 i
i  , imamo važan rezultat:
, imamo važan rezultat:
gde je h dužina normale 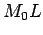 podignute iz tačke
podignute iz tačke 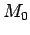 na prečnik
na prečnik 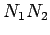 .
Za opštu karakteristiku promene potencije tačke
.
Za opštu karakteristiku promene potencije tačke 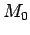 sa rastojanjem
sa rastojanjem 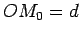 od centra kruga poluprečnika R, može poslužiti sledeća tablica:
od centra kruga poluprečnika R, može poslužiti sledeća tablica:
Teorema 2
Ako jednačinu kruga u Dekartovim koordinatama napi-šemo u obliku:
gde su a,b,c date konstante, onda potencija tačke 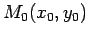 u odnosu na taj krug ima vrednost
u odnosu na taj krug ima vrednost
Uvedimo sad pojam radikalne ose dva kruga.
- Radikalna osa dva data kruga je geometrijsko mesto tačaka, takvih da je vrednost potencije svake takve tačke, u odnosu na jedan krug jednaka vrednosti potencije u odnosu na drugi krug
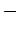 drugim rečima, jednake su dužine tangenata iz svake tačke povučene na jedan i drugi krug (sl. 3). Na slici je prikazan jednostavan način konstrukcije tačke M radikalne ose dva kruga O i
drugim rečima, jednake su dužine tangenata iz svake tačke povučene na jedan i drugi krug (sl. 3). Na slici je prikazan jednostavan način konstrukcije tačke M radikalne ose dva kruga O i 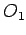 pomoću trećeg kruga
pomoću trećeg kruga 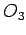 , koji prolazi kroz tačke A, B,
, koji prolazi kroz tačke A, B, 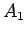 ,
, 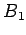 .
.
Teorema 3
Ako su dva kruga data jednačinama
jednačina radikalne ose biće
Ako se dati krugovi seku, ova jednačina je zadovoljena koordinatama presečnih tačaka, pa je radikalna osa prava određena zajedničkom te-tivom, a ako se krugovi dodiruju onda je to zajednička tangenta u dodirnoj tački.
Primer 1
Neka su data dva kruga O i 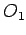 jednačinama:
Jednačina radikalne ose
daje
jednačinama:
Jednačina radikalne ose
daje
gde je 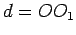 rastojanje centra krugova, a
rastojanje centra krugova, a
- Radikalni centar tri kruga
Teorema 4
1.5
Tri kruga sa centrima
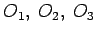 , čiji su poluprečnici
, čiji su poluprečnici
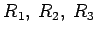 i centralna rastojanja
i centralna rastojanja
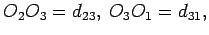
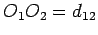 imaju tri radikalne ose, koje ćemo označiti sa
imaju tri radikalne ose, koje ćemo označiti sa
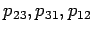 .
.
U opštem slučaju tri radikalne ose za tri kruga seku se u zajedničkoj tački koja se zove radikalni centar tri data kruga.
Ako jednačine krugova izrazimo u obliku
jednačine radikalnih osa se određuju jednačinama ovog sistema:
za
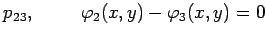
za
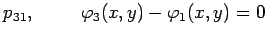
za
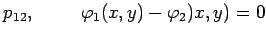
Pošto je svaka od ovih jednačina linearna po x i y, onda vrednosti x i y, koje zadovoljavaju, recimo prve dve jednačine, zadovoljavaju i onu jednačinu koja se dobiva sabiranjem tih jednačina. Međutim, posle takvog sabiranja se dobiva treća jednačina. Na taj način presečna tačka prve dve radikalne ose pripada i trećoj osi. Tri radikalne ose u opštem slučaju imaju samo jednu presečnu tačku koja i služi kao radikalni centar datih krugova.
Treba isključiti specijalne slučajeve. Npr. u slučaju kolinearnosti centara krugova radikalne ose su paralelne i one ne određuju presečnu tačku, drugim rečima one odlaze u beskonačnost.
Oznake
- Dati parametri: tačke A,B,C; prave:
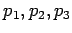 ; krugovi:
; krugovi: 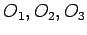 .
.
- Traženi krugovi:
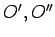 ,
,
- Pomoćne tačke: M,N,P,Q,
 ; pomoćne prave: p,q,r,
; pomoćne prave: p,q,r,  ; pomoćni krugovi:
; pomoćni krugovi:
 ,
, 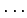 ili
ili
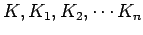 .
.
S i s t e m a t s k a s h e m a z a d a t a k a
s a s k i c a m a (sl.4):
- A B C tri tačke
- A B
 dve tačke i prava
dve tačke i prava
- A B
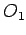 dve tačke i krug
dve tačke i krug

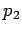 A dve prave i tačka
A dve prave i tačka

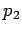
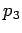 tri prave
tri prave

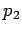
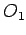 dve prave i krug
dve prave i krug
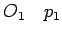 A krug, prava i tačka
A krug, prava i tačka
 A dva kruga i tačka
A dva kruga i tačka
-
 dva kruga i prava
dva kruga i prava
-
 tri kruga
tri kruga
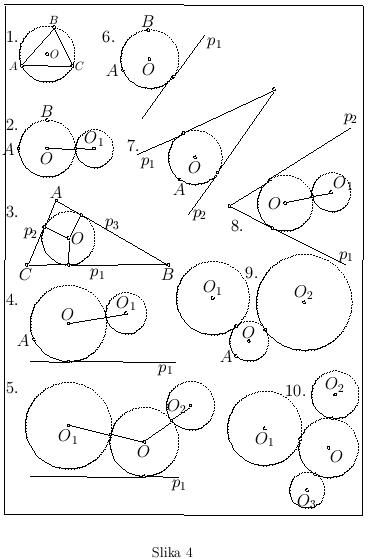
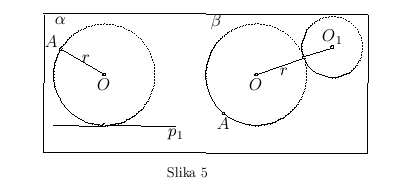
D o p u n s k i z a d a c i (sl. 5)
- A
 r tačka, prava i poluprečnik traženog kruga
r tačka, prava i poluprečnik traženog kruga
 A r krug, tačka i poluprečnik traženog kruga
A r krug, tačka i poluprečnik traženog kruga
Izvođenje svake elementarne geometrijske konsrukcije zasniva se na osnovnim geometrijskim konstrukcijama, na postulatima geometrijskih konstrukcija, koji traže da se u ravni može operisati sa ovim objektima:
- sa tačkom kao presekom dve prave
- sa pravom kroz dve date tačke
- sa krugom datog centra i datog poluprečnika
- i da se mogu odrediti presečne tačke dve prave, prave i kruga i dva kruga, ako takve tačke postoje.
Za konstrukciju, koja se izvodi samo pomoću konačnog broja navedenih osnovnih konstrukcija, kratko se kaže da je izvodljiva samo šestarom i le-njirom. U svojoj čuvenoj knjizi, Grundlagen der Geometrije D.Hilbert1 proučava i aksiomatiku konstruktivnih zadataka.
Pri rešavanju konstruktivnih zadataka u opštem slučaju pojavljuju se ovi poznati delovi potpunog rešenja:
I Proučavanje ili analiza zadataka
II Konstrukcija zadataka
III Dokaz
IV Raspravljanje ili diskusija zadataka
Plan obrade jednog konstruktivnog zadatka, izložen u ova četiri dela, ima ogroman značaj kako u matematičkim naukama, tako uopšte u slučajevima problema, malih i velikih, privatnih i društvenih. Primeri konstruktivnih zadataka jasno pokazuju da je rad bez potpunog plana, npr. samo izvođenje konstrukcije, nedovoljan. Svaki problem je potpuno realan, ako se mogu postići odgovarajući rezultati u svakom delu skiciranog plana. To se prime-njuje i na opšte probleme sa odgovarajućim promenama u vezi sa prirodom zadataka.
2005-04-12



![]() rastojanje centra krugova, a
rastojanje centra krugova, a

