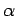
Naći krug datog poluprečnika, koji prolazi kroz datu tačku i dodiruje datu pravu
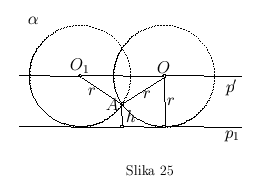
Neka su dati: tačka A, prava  i dužina r jednaka poluprečniku traženog kruga (sl. 25). Treba kroz tačku A povući krug poluprečnika r, koji dodiruje pravu
i dužina r jednaka poluprečniku traženog kruga (sl. 25). Treba kroz tačku A povući krug poluprečnika r, koji dodiruje pravu  .
.
- Analiza: Pretpostavimo da krug O dodiruje pravu
 i prolazi kroz tačku A. Ako tada povučemo pravu
i prolazi kroz tačku A. Ako tada povučemo pravu 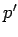 paralelnu sa
paralelnu sa  , na odstojanju r od prave
, na odstojanju r od prave  i to sa strane gde se nalazi tačka A, onda se može tvrditi da se tačka O - centar traženog kruga nalazi
i to sa strane gde se nalazi tačka A, onda se može tvrditi da se tačka O - centar traženog kruga nalazi
1. na pravoj 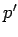
2. na krugu poluprečnika r, sa centrom u tački A.
- Konstrukcija: Povucimo na rastojanju od prave
 , sa iste strane sa koje je tačka A, pravu
, sa iste strane sa koje je tačka A, pravu 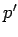 paralelnu pravoj
paralelnu pravoj  . Iz tačke A, kao centra, poluprečnikom r opišemo krug A. Neka on seče pravu
. Iz tačke A, kao centra, poluprečnikom r opišemo krug A. Neka on seče pravu 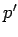 u tačkama O i
u tačkama O i 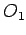 . Krugovi O i
. Krugovi O i 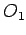 poluprečnika r odgovaraju uslovima zadatka.
poluprečnika r odgovaraju uslovima zadatka.
- Dokaz: Oba kruga prolaze kroz tačku A. Svaki od njih dodiruje pravu
 , jer je rastojanje njihovih centara od te prave jednako poluprečniku kruga. Najzad, svaki ima za poluprečnik datu dužinu r.
, jer je rastojanje njihovih centara od te prave jednako poluprečniku kruga. Najzad, svaki ima za poluprečnik datu dužinu r.
- Diskusija: Pri diskusiji ovog zadatka možemo pretpostaviti da je veličina r stalna, jer uvek možemo sliku crtati tako da veličina r ostane ista.
Prema tome, dovoljno je menjati samo vrednost odstojanja tačke A od date prave
 , koje možemo označiti sa h. Dovoljno je diskutovati samo pozitivne vrednosti h, jer negativnim vrednostima odgovara rešenje istog zadatka, samo sa položajem tačke A sa druge strane od prave
, koje možemo označiti sa h. Dovoljno je diskutovati samo pozitivne vrednosti h, jer negativnim vrednostima odgovara rešenje istog zadatka, samo sa položajem tačke A sa druge strane od prave  .
.
- Ako je 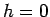 , tačka A leži na pravoj
, tačka A leži na pravoj  . Centri O i
. Centri O i  se poklapaju i leže na normali iz tačke A na rastojanju r od prave
se poklapaju i leže na normali iz tačke A na rastojanju r od prave  . Prema tome, postoji jedno rešenje.
. Prema tome, postoji jedno rešenje.
- Ako uzmemo u obzir i drugu stranu ravni od prave  , možemo tvrditi da u njoj možemo konstruisati dva kruga poluprečnika r, koji prolaze kroz tačku A i dodiruju datu pravu.
, možemo tvrditi da u njoj možemo konstruisati dva kruga poluprečnika r, koji prolaze kroz tačku A i dodiruju datu pravu.
- Ako je 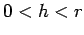 , tada postoje dva rešenja (sl. 25. a)
, tada postoje dva rešenja (sl. 25. a)
- Ako je 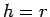 , tačka A se nalazi na pravoj
, tačka A se nalazi na pravoj 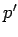 , pa postoje dva rešenja, pri čemu se krugovi O i
, pa postoje dva rešenja, pri čemu se krugovi O i 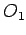 dodiruju u tački A.
dodiruju u tački A.
- Ako je 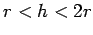 , ponovo postoje dva preseka krugova O i
, ponovo postoje dva preseka krugova O i 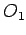 , ali uslovima zadatka odgovara samo gornja tačka A.
, ali uslovima zadatka odgovara samo gornja tačka A.
- Ako je 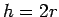 , tačke O i
, tačke O i 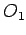 ponovo se poklapaju. Traženi krug ima za prečnik dužinu normale, konstruisanu iz tačke A na pravu
ponovo se poklapaju. Traženi krug ima za prečnik dužinu normale, konstruisanu iz tačke A na pravu  . Dakle, postoji jedno rešenje.
. Dakle, postoji jedno rešenje.
- Ako je 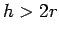 , tada krug iz centra A ne seče pravu p, tj. taj slučaj nije moguć.
, tada krug iz centra A ne seče pravu p, tj. taj slučaj nije moguć.
Rezultat diskusije može se predstaviti sledećom tabelom:
2005-04-12
![]() i dužina r jednaka poluprečniku traženog kruga (sl. 25). Treba kroz tačku A povući krug poluprečnika r, koji dodiruje pravu
i dužina r jednaka poluprečniku traženog kruga (sl. 25). Treba kroz tačku A povući krug poluprečnika r, koji dodiruje pravu ![]() .
.
